15 Vektorikentän muodostaminen lähde- ja pyörrekentästä
15.1 Lähteiden synnyttämä vektorikenttä
Tehtävä 433
Pyörteettömän vektorikentän u(r) lähdealueena on origokeskinen R-säteinen pallo. Tämän sisäpuolella lähdekenttä on
(r) = R - r ja ulkopuolella siis (r) = 0. Laske
kenttä päättelemällä ensin sen muodoksi symmetrian perusteella u(r) = f(r)r ja
laskemalla sen jälkeen f(r) soveltamalla Gaussin lausetta r-säteiseen palloon. Mikä on
kenttävektorin itseisarvon maksimi?
Tehtävä 434
Pyörteettömän vektorikentän u lähdealueena on molempiin suuntiin ääretön R-säteinen ympyrälieriö, jonka sisällä lähdekenttä on c(R - r), missä c on vakio ja r etäisyys lieriön akselista. Määritä kenttä u sekä lieriön sisä- että ulkopuolella.Tehtävä 435
Pyörteettömän pallosymmetrisen vektorikentän lähdetiheys on r-5/2 , missä r on etäisyys origosta. Laske pallokoorinaateissa kenttä ja vastaava potentiaali. Osoita, että potentiaali toteuttaa Poissonin differentiaaliyhtälön.Tehtävä 436
Pyörteettömän pallosymmetrisen vektorikentän lähdetiheys on e-r, missä r on etäisyys origosta. Määritä kenttä.Tehtävä 437
Pyörteettömän vektorikentän u lähdetiheys pallokoordinaateissa on
(r) =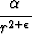 
, 
, 
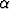vakioita, 0 < < 1.
Määritä kenttä ja vastaava potentiaali pallokoordinaateissa sekä osoita laskemalla, että potentiaali toteuttaa Poissonin differentiaaliyhtälön.
Tehtävä 438
Origon suhteen pallosymmetrisen lähdekentän synnyttämän pyörteettömän
vektorikentän u potentiaali on
V (r) =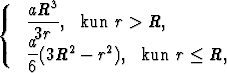 
missä a ja R ovat vakioita. Määritä u ja .
Tehtävä 439
Origon suhteen pallosymmetrisen lähdekentän synnyttämän pyörteettömän
vektorikentän u potentiaali on V = e-r2. Määritä u ja .
Tehtävä 440
Origon suhteen pallosymmetrisen lähdekentän synnyttämän pyörteettömän
vektorikentän u potentiaali on V = e-r3. Määritä u ja tutki lähdekentän positiivisuutta
ja negatiivisuutta.
Tehtävä 441
Origon suhteen pallosymmetrisen lähdekentän synnyttämä potentiaali on V = -ke-r2 , missä k on positiivinen vakio. Millä etäisyydellä origosta lähdetiheys on suurin?Tehtävä 442
Pyörteettömän vektorikentän lähdealueena on R-säteinen pallo. Kentän potentiaali pallon sisäpuolisissa pisteissä on V (r) = 2R - r3/R2, missä r on etäisyys pallon keskipisteestä. Määritä lähdetiheys.Tehtävä 443
Pyörteettömän kentän u lähdealueena on xy-tason neliö 0 < x < a, 0 < y < a, jossa lähteen pintatiheys on xy. Laske potentiaali V z-akselin pisteissä. Miten suhtautuvat toisiinsa V (0, 0, a) ja V (0, 0, -a)?Tehtävä 444
Pyörteettömän vektorikentän u lähdealue on xy-tasossa: { (x, y, 0) | 1 < x2 + y2 < 5, x > 0 }. Lähteen pintatiheys on vakio = 1. Määritä kenttä origossa.Tehtävä 445
Pyörteettömän vektorikentän u lähdealueena on puolipallon pinta: x2 + y2 + z2 = R2, z > 0. Lähteen pintatiheys on vakio. Kentän potentiaali olkoon V . Laske V (0, 0, -R) - V (0, 0, 0).15.2 Pyörteiden synnyttämä vektorikenttä
Tehtävä 446
Pyörreviiva, jonka vuo on I, muodostuu y-akselin ja x-akselin positiivisista osista. Edellisellä pyörrekentän suunta on -j, jälkimmäisellä i. Laske syntyvä lähteetön kenttä u(r) z-akselin pisteissä.Tehtävä 447
Umpinainen pyörreviiva, jonka pituus on 12a ja vuo I, kulkee kuution { (x, y, z) | |x| < a, |y| < a, |z| < a } särmiä pitkin käymällä kaikissa kuution kärjissä paitsi pisteissä (a, a, a) ja (-a, -a, -a). Määritä sen synnyttämä kenttä kuution keskipisteessä.15.3 Lähteistä ja pyörteistä syntyvän kentän yksikäsitteisyys
Tehtävä 448
Massapisteen aiheuttamasta gravitaatiokentästä oletetaan, että se on pallosymmetrinen, lähteetön ja pyörteetön massapisteen ulkopuolella sekä häviää äärettömyydessä. Osoita, että kenttä on välttämättä muotoa
u(r) =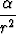 
r0,
missä 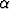on vakio.
Tehtävä 449
Massapisteen aiheuttaman gravitaatiokentän potentiaali u(x, y, z) toteuttaa massapisteen ulkopuolella Laplacen differentiaaliyhtälön
+ 
+ 
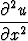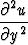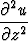= 0.
On luonnollista olettaa, että kenttä on pallosymmetrinen, ts. u(x, y, z) = f(r), kun massa sijaitsee origossa. Määritä kaikki mahdolliset potentiaalifunktiot.