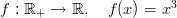Funktiokäsite

Funktio on matematiikan tärkeimpiä käsitteitä. Yksinkertaisin funktiotyyppi liittää reaalilukuun x toisen reaaliluvun y. Liittäminen ilmaistaan lausekkeella, jossa y lausutaan x:n avulla, esimerkiksi y = x + sin(x). Tällainen funktio voidaan esittää xy-tasoon piirretyllä kuvaajalla, joka muodostuu pisteistä (x,y), missä x saa kaikki arvot funktion määrittelyjoukosta.
Funktiot voivat kuitenkin olla paljon monimutkaisemmin määriteltyjä. Lukujen x ja y välinen riippuvuus voi perustua integraalilausekkeeseen, se voi syntyä differentiaaliyhtälön ratkaisusta jne. Esimerkiksi fysiikassa esiintyy paljon tällä tavoin määriteltyjä funktioita.
Funktion käsite on kuitenkin vielä yleisempi. Funktion f : A → B lähtöjoukko A ja maalijoukko B voivat olla mitä tahansa joukkoja, ja joukkoon A kuuluvan alkion x kuva y voidaan määritellä millä tahansa yksikäsitteisellä tavalla, ei mitenkään välttämättä lausekkeella.
 Funktiokäsitteen määrittely
Funktiokäsitteen määrittely Esimerkkejä funktioista
Esimerkkejä funktioista Reaalifunktion käsite, alkeisfunktiot
Reaalifunktion käsite, alkeisfunktiot
Kahdesta funktiosta voidaan muodostaa uusi funktio yhdistämällä ne. Jos jokaista funktion arvoa y vastaa täsmälleen yksi x, funktiolla on käänteisfunktio.
 Yhdistetty funktio
Yhdistetty funktio Surjektio, injektio, bijektio
Surjektio, injektio, bijektio Käänteisfunktio
Käänteisfunktio

Esimerkkejä
- Olkoot annettiuna joukko Kääpiöt, joka sisältää Lumikin
seitsemän kääpiötä, Kääpiöt = {Viisas, Jörö, Lystikäs,
Unelias, Ujo, Nuhanenä, Vilkas} sekä luonnollisten lukujen joukko
 . Voidaan muodostaa kuvaus eli funktio kääpiöiden ja
luonnollisten lukujen välille esimerkiksi liittämällä jokaiseen
kääpiöön sen nimen kirjainten lukumäärän. (Merkitään
kuvausta vaikka
. Voidaan muodostaa kuvaus eli funktio kääpiöiden ja
luonnollisten lukujen välille esimerkiksi liittämällä jokaiseen
kääpiöön sen nimen kirjainten lukumäärän. (Merkitään
kuvausta vaikka  .) Esimerkiksi kääpiöön Ujo
kuvaus liittää luvun kolme:
.) Esimerkiksi kääpiöön Ujo
kuvaus liittää luvun kolme:  . Kuvaus ei kuitenkaan ole
injektio sillä
. Kuvaus ei kuitenkaan ole
injektio sillä  . Kuvaus ei ole surjektiokaan,
sillä kuvaus ei liitä kaikkia luonnollisia lukuja kääpiöihin. Jos
rajoitamme maalijoukon joukoksi
. Kuvaus ei ole surjektiokaan,
sillä kuvaus ei liitä kaikkia luonnollisia lukuja kääpiöihin. Jos
rajoitamme maalijoukon joukoksi  , niin saamme
kuvauksesta
, niin saamme
kuvauksesta  surjektion.
surjektion.
- Muodostetaan yhdistettyjä kuvauksia funktioilla
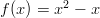 ja
ja
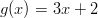 .
.
Valitaan ulkofunktioksi ja
ulkofunktioksi ja 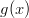 sisäfunktioksi, eli sijoitetaan
sisäfunktioksi, eli sijoitetaan
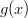 ulkofunktion muuttujan paikalle.
ulkofunktion muuttujan paikalle.
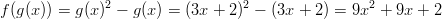
Muodostetaan vastaavasti myös pari muuta yhdistettya kuvausta.
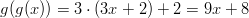

- Olkoon
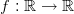 ,
,  .
.
Kuvaus on surjektio. Jos valitaan mielivaltainen alkio sille
pätee:
sille
pätee:
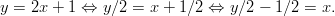
Riippumatta siitä minkä
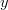 :n maalijoukosta valitsee tälläinen
:n maalijoukosta valitsee tälläinen
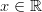 löytyy aina.
löytyy aina.
Kuvaus on myös injektio. Valitaan mielivaltaiset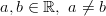 , niille
pätee:
, niille
pätee:
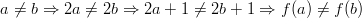
Injektiivisyyden voi todistaa myös lähtemällä oletuksesta
 ja päätymällä lopputulokseen
ja päätymällä lopputulokseen 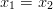 .
.
Koska kuvaus on injektio sekä surjektio, se on bijektio.
- Tarkastellaan edellisen esimerkin käänteiskuvaajaa. Tämä on
mahdollista, koska
 on bijektio. Funktio
on bijektio. Funktio 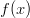 saa pisteessa
saa pisteessa
 arvon
arvon 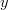 , eli tarvitsee selvittää milloin
, eli tarvitsee selvittää milloin 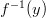 saa arvon
saa arvon
 .
.
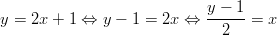
Funktion käänteiskuvaus on
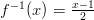 .
.
- Olkoon
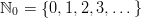 ja
ja 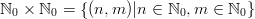 .
Kuvaus
.
Kuvaus 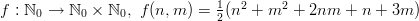 on
bijektio, joka kuvaa luonnolisista luvuista muodostettuja lukupareja
luonnollisille luvuille.
on
bijektio, joka kuvaa luonnolisista luvuista muodostettuja lukupareja
luonnollisille luvuille.


Harjoitustehtäviä
- Muodosta
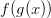 ,
,  ja
ja  , kun
, kun
-
- Onko funktio
 injektio, surjektio tai bijektio? Muodosta myös
käänteiskuvaus, jos mahdollista.
injektio, surjektio tai bijektio? Muodosta myös
käänteiskuvaus, jos mahdollista.
-
Tehtävien vastaukset:

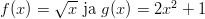
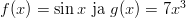
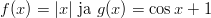
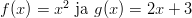
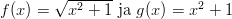
![] π π[ f : − 2 ,2 → ℝ, f (x) = tanx](funktio45x.gif)