Sisällön pääryhmät Funktio Funktiokäsite [ 1 2 3 4 5 6 ] ESITIEDOT: KATSO MYÖS:  reaalifunktiot,  joukko-oppi

Kansisivu  Sisältö  Hakemisto

Funktio f joukosta A joukkoon B tarkoittaa sääntöä, joka jokaiseen joukon A alkioon liittää jonkin alkion joukosta B. Yleensä merkitään f : A B.

Jos x on joukon A alkio (merkitään x A) ja y tähän liittyvä joukon B alkio (y B), merkitään y = f(x) ja sanotaan, että funktio f kuvaa alkion x alkiolle y tai että y on alkion x kuva funktiossa f.

Joukko A on funktion f lähtöjoukko eli määrittelyjoukko ja B sen maalijoukko.

Joskus käytetään sanaa kuvaus synonyymina funktiolle. (Toisinaan sillä voi kyllä olla myös hieman funktion käsitteestä poikkeava merkitys.)

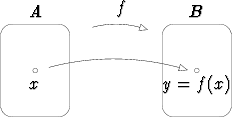
Funktion lähtö- tai maalijoukon ei tarvitse olla lukujoukko. Varsin luonnollinen joukkotyyppi on vaikkapa vektorijoukko. Varsinkin lukujoukkojen tapauksessa funktio annetaan usein ilmoittamalla sen lauseke, mutta muitakin mahdollisuuksia on.

joukko  alkio  vektori

Kivelä, niinkuin matematiikka, versio 1.12