Sisällön pääryhmät Diskreettiä matematiikkaa Joukko-oppi [ 1 2 3 4 ] ESITIEDOT: KATSO MYÖS:  logiikka,  reaaliluvut

Kansisivu  Sisältö  Hakemisto

Matemaattisen päättelyn (todistamisen) pohjana pidetään usein formaalin logiikan ohella joukko-oppia. Vaikka näkemystä voidaankin kritisoida eikä joukko-oppi ole lähtökohtana ongelmaton eikä aina tarpeellinenkaan, on peruskäsitteiden tuntemus kuitenkin välttämätöntä.

Joukko on jonkinlainen kokoelma tarkasteltavana olevan perusjoukon objekteja eli alkioita.

Tyypillisiä perusjoukkoja ovat reaalilukujoukko , kompleksilukujoukko 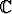tai vaikkapa reaalimuuttujan reaaliarvoisten funktioiden f : joukko.

Perusjoukossa voidaan muodostaa esimerkiksi joukko, joka koostuu positiivisista reaaliluvuista. Jos tälle käytetään nimeä ₊, merkitään 2 ₊ ja -2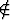₊ osoittamaan, että luku 2 kuuluu joukkoon ja luku -2 ei kuulu; vaihtoehtoisesti voidaan sanoa, että 2 on alkiona ko. joukossa, tms.

Joukkoja merkitään yleensä isoilla kirjaimilla ja niiden määrittelyssä käytetään aaltosulkumerkintää seuraavaan tapaan:

A = {x | x² > 2}.

Pystyviivan vasemmalla puolella osoitetaan, että perusjoukkona on reaaliluvut . Oikealla puolella on joukon alkioilta vaadittava ehto. Esimerkin joukkoon A siis kuuluvat reaaliluvut, jotka ovat > 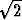tai < -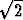. Jos asiayhteydestä on selvää, mistä perusjoukosta on kyse, merkitään lyhyemmin: {x | x² > 2}.

Jos joukossa on äärellisen monta alkiota, se voidaan antaa luettelemalla alkiot. Esimerkiksi A = {1, 3, 5, 7} on neljän alkion (luvun) muodostama joukko.

Joukko voi luonnollisesti käsittää kaikki perusjoukon alkiot. Toisaalta puhutaan myös tyhjästä joukosta, jossa ei ole ainuttakaan alkiota. Tätä merkitään symbolilla Ø. Esimerkiksi {x | x² > 0} = , {x | x² < 0} = Ø.

Muita esimerkkejä joukkomerkinnän käytöstä ovat kompleksitason origokeskinen R-säteinen ympyrä {z 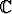| |z| < R} ja sellaisten jatkuvien reaalifunktioiden joukko, joiden kuvaaja kulkee origon kautta:

{f : | f jatkuva,  f(0) = 0}.

logiikka  reaaliluku  kompleksiluku  funktio  funktio (reaali-)  kompleksitaso  itseisarvo (kompleksiluvun)  jatkuvuus

Kivelä, niinkuin matematiikka, versio 1.12