![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Luvut
Luvut  Kompleksiluvut [ 1 2 3 4 5 6
]
Kompleksiluvut [ 1 2 3 4 5 6
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaaliluvut
reaaliluvut
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) polynomien tekijöihin jako,
polynomien tekijöihin jako, ![[#]](kuvat/msam10-c-4.gif) vektori
vektori
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Luvut Luvut  Kompleksiluvut [ 1 2 3 4 5 6
] Kompleksiluvut [ 1 2 3 4 5 6
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaaliluvut reaaliluvut
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) polynomien tekijöihin jako, polynomien tekijöihin jako, ![[#]](kuvat/msam10-c-4.gif) vektori vektori
|
|
Lukukäsitteen vaiheittainen laajennus johtaa luonnollisista luvuista kokonaislukujen ja rationaalilukujen kautta reaalilukuihin. Jokaisessa vaiheessa ratkeavien yhtälöiden määrä lisääntyy: yhtälö x + 2 = 0 ei ratkea luonnollisten lukujen joukossa, mutta kylläkin kokonaislukujoukossa; yhtälöllä 3x = 2 ei ole kokonaislukuratkaisua, mutta rationaalinen ratkaisu sillä on; yhtälön x2 - 2 = 0 ratkeavuus edellyttää rationaalilukujoukon laajentamista reaalilukujoukoksi.
Jokaisessa vaiheessa uusi lukujoukko on edellisen laajennus: edeltäjä on uuden joukon osajoukko. Prosessia voidaan jatkaa. Yhtälöllä x2 + 1 = 0 ei ole ratkaisua reaalilukujoukossa, mutta laajentamalla reaalilukujoukko edelleen kompleksilukujen joukoksi tällekin yhtälölle (ja samalla kaikille polynomiyhtälöille) löydetään ratkaisu.
Formaalisti laskemalla yhtälön ratkaisuksi saataisiin x = ±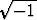 . Ongelmaksi
tällöin jää, mitä itse asiassa tarkoittaa
. Ongelmaksi
tällöin jää, mitä itse asiassa tarkoittaa 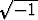 , jolle käytetään myös merkintää i.
Vaikka tarkastelua voitaisiin tältäkin pohjalta jatkaa, saattaa olla luonnollisempaa
suorittaa laajennus geometrisesti:
, jolle käytetään myös merkintää i.
Vaikka tarkastelua voitaisiin tältäkin pohjalta jatkaa, saattaa olla luonnollisempaa
suorittaa laajennus geometrisesti:
Lukusuora  sijoitetaan xy-tason x-akseliksi ja koko xy-tasoa aletaan kutsua
kompleksitasoksi. Sen pisteet (x, y) ovat kompleksilukuja. Näiden muodostama
joukko — siis itse asiassa xy-taso — on kompleksilukujen joukko, symbolina
sijoitetaan xy-tason x-akseliksi ja koko xy-tasoa aletaan kutsua
kompleksitasoksi. Sen pisteet (x, y) ovat kompleksilukuja. Näiden muodostama
joukko — siis itse asiassa xy-taso — on kompleksilukujen joukko, symbolina
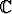 .
.
Reaaliluvut ovat x-akselilla olevia pisteitä, so. muotoa (x, 0). Muut pisteet ovat imaginaarilukuja. Tilanne on siten samankaltainen kuin aikaisemmin: edeltävä lukujoukko on uuden osajoukko.
Näkemys kompleksiluvuista xy-tason pisteinä on peräisin 1700- ja 1800-lukujen vaihteen ajalta. Kompleksilukujen historian voidaan kuitenkin katsoa alkavan lähes kolme sataa vuotta aikaisemmin polynomiyhtälöiden ratkaisujen tutkimisesta.
![[#]](kuvat/msam10-c-4.gif) luonnollinen luku luonnollinen luku![[#]](kuvat/msam10-c-4.gif) kokonaisluku kokonaisluku![[#]](kuvat/msam10-c-4.gif) rationaaliluku rationaaliluku![[#]](kuvat/msam10-c-4.gif) reaaliluku reaaliluku![[#]](kuvat/msam10-c-4.gif) yhtälö yhtälö![[#]](kuvat/msam10-c-4.gif) yhtälö
(polynomi-) yhtälö
(polynomi-)![[#]](kuvat/msam10-c-4.gif) osajoukko osajoukko![[#]](kuvat/msam10-c-4.gif) yhtälö (polynomi-) yhtälö (polynomi-)![[#]](kuvat/msam10-c-4.gif) lukusuora lukusuora![[#]](kuvat/msam10-c-4.gif) koordinaatisto (xy-) koordinaatisto (xy-) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12