![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Luvut
Luvut  Kompleksiluvut [ 1 2 3 4 5 6
]
Kompleksiluvut [ 1 2 3 4 5 6
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaaliluvut
reaaliluvut
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) polynomien tekijöihin jako,
polynomien tekijöihin jako, ![[#]](kuvat/msam10-c-4.gif) vektori
vektori
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Luvut Luvut  Kompleksiluvut [ 1 2 3 4 5 6
] Kompleksiluvut [ 1 2 3 4 5 6
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaaliluvut reaaliluvut
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) polynomien tekijöihin jako, polynomien tekijöihin jako, ![[#]](kuvat/msam10-c-4.gif) vektori vektori
|
|
Jotta laskusäännöt olisivat voimassa ja lisäksi olisi i2 = -1, on kertolaskun ilmeisestikin tapahduttava seuraavasti:
| (x1, y1) . (x2, y2) | = | (x1 + y1i) . (x2 + y2i) | ||
| = | x1x2 + y1y2i2 + x1y2i + x2y1i | |||
| = | (x1x2 - y1y2) + (x1y2 + x2y1)i | |||
| = | (x1x2 - y1y2, x1y2 + x2y1). |
(x1, y1) . (x2, y2) = (x1x2 - y1y2, x1y2 + x2y1).
Tällöin on todellakin i2 = -1:
i . i = (0, 1) . (0, 1) = (0 . 0 - 1 . 1, 0 . 1 + 0 . 1) = (-1, 0) = -1.
Kaikki tavanomaiset algebran laskusäännöt (yhteen- ja kertolaskun vaihdannaisuus ja liitännäisyys, osittelulait) ovat voimassa, kuten määritelmiin perustuvilla mekaanisilla — tosin paikoin pitkillä — laskuilla voidaan todeta.
Myös jakolasku tulee mahdolliseksi, jos jakaja poikkeaa nollasta, ts. ei ole kompleksiluku (0, 0). Murtoluvuksi kirjoitettu osamäärä on yksinkertaisesti lavennettava nimittäjän liittoluvulla. Esimerkki edempänä.
Kompleksilukuja ei määrittelyn jälkeen ole tapana merkitä lukupareina (x, y), vaan käytetään esitysmuotoa x + yi. Yhteen-, vähennys- ja kertolaskut kompleksilukualgebrassa suoritetaan tällöin tavanomaisilla algebran laskusäännöillä. Tarvittaessa käytetään sieventämiseen yhtälöä i2 = -1.
Kaikilta osin ei kompleksiluvuilla laskeminen kuitenkaan suju samoin kuin
reaalialueella. Esimerkiksi juurenotossa on oltava varovainen. Mm. neliöjuuren
positiivista haaraa ei voida määritellä. Yritys kirjoittaa i = +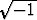 johtaa
ristiriitaan:
johtaa
ristiriitaan:
-1 = i2 = (+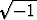 )(+
)(+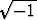 ) = +
) = +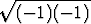 = +
= +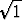 = +1.
= +1.
![[#]](kuvat/msam10-c-4.gif) laskulaki (summa ja tulo) laskulaki (summa ja tulo)![[#]](kuvat/msam10-c-4.gif) vaihdannaisuus vaihdannaisuus![[#]](kuvat/msam10-c-4.gif) liitännäisyys liitännäisyys![[#]](kuvat/msam10-c-4.gif) osittelulaki osittelulaki![[#]](kuvat/msam10-c-4.gif) laventaminen laventaminen![[#]](kuvat/msam10-c-4.gif) nimittäjä nimittäjä![[#]](kuvat/msam10-c-4.gif) juuri (murtopotenssi) juuri (murtopotenssi)![[#]](kuvat/msam10-c-4.gif) juurifunktio juurifunktio![[#]](kuvat/msam10-c-4.gif) neliöjuuri neliöjuuri |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12