![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Potenssit ja polynomit
Potenssit ja polynomit  Juuret [ 1 2 3
]
Juuret [ 1 2 3
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) potenssi
potenssi
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot,
reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) kompleksiluvut
kompleksiluvut
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Potenssit ja polynomit Potenssit ja polynomit  Juuret [ 1 2 3
] Juuret [ 1 2 3
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) potenssi potenssi
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot, reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) kompleksiluvut kompleksiluvut
|
|
Luvun x n:nnelle juurelle käytetään merkintää 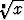 . Luku x on juurrettava, luku n
on juuren indeksi.
. Luku x on juurrettava, luku n
on juuren indeksi.
Koska juurella kuitenkin on yleensä useita arvoja, kiinnitetään merkintä tarkoittamaan yhtä niistä. Tällöin puhutaan juurifunktiosta tai juuren päähaarasta.
Jos juurrettava x on positiivinen, on kaikilla juurilla ainakin reaalinen ja
positiivinen arvo. Merkintä 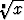 tarkoittaa tätä. Sama asia voidaan ilmaista myös
potenssifunktion avulla:
tarkoittaa tätä. Sama asia voidaan ilmaista myös
potenssifunktion avulla: 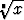 = x1/n.
= x1/n.
Aina on myös 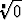 = 0.
= 0.
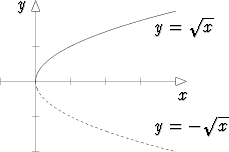
Esimerkiksi (reaalinen) neliöjuurifunktio 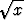 — lyhyemmin yleensä neliöjuuri —
määritellään vain, kun x on reaalinen ja > 0. Kahdesta mahdollisesta neliöjuuren
arvosta valitaan positiivinen, jolloin esimerkiksi
— lyhyemmin yleensä neliöjuuri —
määritellään vain, kun x on reaalinen ja > 0. Kahdesta mahdollisesta neliöjuuren
arvosta valitaan positiivinen, jolloin esimerkiksi 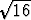 = +4. Seurauksena on
kaikille reaaliluvuille a laskusääntö
= +4. Seurauksena on
kaikille reaaliluvuille a laskusääntö 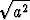 = |a|, koska a2 on aina > 0 ja juuri siis
voidaan muodostaa, mutta a itse voi olla negatiivinenkin.
= |a|, koska a2 on aina > 0 ja juuri siis
voidaan muodostaa, mutta a itse voi olla negatiivinenkin.
Neliöjuurella on myös negatiivinen haara, funktion ns. sivuhaara, jolloin funktion
arvoksi valitaan negatiivinen vaihtoehto. Sivuhaaran mukaan laskien on
reaaliluvun x > 0 neliöjuuri -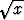 .
.
Laskimien ja tietokoneohjelmien neliöjuurifunktiot toimivat ainakin numeerisia arvoja laskettaessa poikkeuksetta positiivisen haaran (päähaaran) mukaisesti. Lausekkeita käsiteltäessä asia ei kaikissa tietokoneohjelmissa ole yhtä selvä, vaan saattaa jäädä käyttäjän vastuulle.
Yleisesti: Jos x on reaalinen ja > 0, tarkoittaa 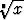 sitä n:ttä juurta, joka on
reaalinen ja > 0.
sitä n:ttä juurta, joka on
reaalinen ja > 0.
Jos n on pariton, tämä on juurifunktion ainoa (reaalinen) haara. Jos n on
parillinen, juurifunktiolla on myös negatiivinen haara -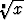 .
.
![[#]](kuvat/msam10-c-4.gif) funktio funktio![[#]](kuvat/msam10-c-4.gif) potenssi (murto-) potenssi (murto-)![[#]](kuvat/msam10-c-4.gif) potenssifunktio potenssifunktio![[#]](kuvat/msam10-c-4.gif) reaaliluku reaaliluku |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12