Sisällön pääryhmät Potenssit ja polynomit Potenssi [ 1 2 3 4 ] ESITIEDOT: KATSO MYÖS:  juuret,  reaalifunktiot,  kompleksiluvut

Kansisivu  Sisältö  Hakemisto

Olkoon tavoitteena määritellä potenssi x, missä kantaluku x ja eksponentti ovat mitä tahansa reaalilukuja. Määrittely tapahtuu useassa vaiheessa eikä tavoitteeseen täydelleen päästä: kantalukua x joudutaan jossakin määrin rajoittamaan.

1) Olkoon aluksi eksponentti luonnollinen luku n, ts. n on kokonaisluku ja > 1. Tällöin asetetaan

xⁿ = .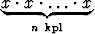

Kantaluku x voi olla mikä tahansa reaaliluku. Selvästikin on voimassa kertolaskusääntö x^n . x^m = x^n+m ja potenssiinkorotussääntö (xⁿ)^m = x^nm.

2) Jos eksponentti on negatiivinen, määritellään

x^-n = .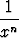

Tällöin tulee luonnollisesti olla x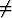0.

Motiivina määrittelyssä on halu säilyttää em. potenssien kertolaskusääntö voimassa: Onhan nimittäin elementaarien supistussääntöjen mukaisesti esimerkiksi x⁵/x³ = x², x³/x⁵ = 1/x² ja nämä voidaan eo. määrittelyn turvin kirjoittaa x^5 . x^-3 = x², x^3 . x^-5 = x^-2, jolloin laskusääntö säilyy voimassa.

3) Jos on n = 0, määritellään

x⁰ = 1.

Motiivina on triviaali yhtälö xⁿ/xⁿ = 1, jonka vasen puoli kohdan 2 mukaan laskien saa muodon x^n-n = x⁰. Jotta murtolauseke xⁿ/xⁿ ei saisi epämääräistä muotoa 0/0, on oletettava x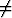0.

Potenssi on siis saatu määritellyksi kaikille kokonaislukueksponenteille.

reaaliluku  luonnollinen luku  kokonaisluku  supistaminen

Kivelä, niinkuin matematiikka, versio 1.12