![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Luvut
Luvut  Reaaliluvut [ 1 2 3 4 5 6 7
]
Reaaliluvut [ 1 2 3 4 5 6 7
]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) murtoluvut,
murtoluvut, ![[#]](kuvat/msam10-c-4.gif) lukujärjestelmät,
lukujärjestelmät, ![[#]](kuvat/msam10-c-4.gif) kompleksiluvut
kompleksiluvut
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Luvut Luvut  Reaaliluvut [ 1 2 3 4 5 6 7
] Reaaliluvut [ 1 2 3 4 5 6 7
]
ESITIEDOT: KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) murtoluvut, murtoluvut, ![[#]](kuvat/msam10-c-4.gif) lukujärjestelmät, lukujärjestelmät, ![[#]](kuvat/msam10-c-4.gif) kompleksiluvut kompleksiluvut
|
|
Lukukäsitteen määrittelyn lähtökohtana on lukumäärän ilmaisemiseen tarvittava luonnollisten lukujen joukko:
1, 2, 3, 4, 5, ... .
Toisinaan myös 0 (nolla) liitetään tähän joukkoon, ts. sitäkin pidetään
luonnollisena lukuna. Kyse on sopimuksesta: joissakin yhteyksissä on
käytännöllistä ottaa nolla mukaan, toisissa ei. Periaatteessa molemmat ovat
yhtä hyviä ratkaisuja. Luonnollisten lukujen joukolle käytetään symbolia
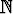 .
.
Kokonaisuuksien osien tarkastelu johtaa murtolukuihin: puolet matkasta; kaksi kolmasosaa palkasta. Toisaalta monien suureiden tarkastelu johtaa myös negatiivisiin lukuihin: pakkasta on viisi astetta, ts. lämpötila on -5o; hidastuvuus on negatiivista kiihtyvyyttä.
Liittämällä luonnollisiin lukuihin vastaavat negatiiviset luvut (ja nolla), saadaan
kokonaisluvut: ..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, .... Kokonaislukujoukon
symboli on 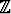 .
.
Rationaaliluvut saadaan liittämällä mukaan positiiviset ja negatiiviset murtoluvut,
so. muotoa p/q olevat luvut, missä p on (positiivinen tai negatiivinen)
kokonaisluku ja q luonnollinen luku (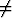 0). Tällöin kahta rationaalilukua pidetään
samoina, jos toinen saadaan toisesta laventamalla tai supistamalla:
0). Tällöin kahta rationaalilukua pidetään
samoina, jos toinen saadaan toisesta laventamalla tai supistamalla:
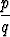 =
= 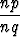 ,
,
missä n on kokonaisluku, n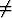 0. Rationaalilukujoukon symboli on
0. Rationaalilukujoukon symboli on 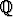 .
.
![[#]](kuvat/msam10-c-4.gif) joukko joukko![[#]](kuvat/msam10-c-4.gif) murtoluku murtoluku![[#]](kuvat/msam10-c-4.gif) laventaminen laventaminen |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12