![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Luvut
Luvut  Reaaliluvut [ 1 2 3 4 5 6 7
]
Reaaliluvut [ 1 2 3 4 5 6 7
]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) murtoluvut,
murtoluvut, ![[#]](kuvat/msam10-c-4.gif) lukujärjestelmät,
lukujärjestelmät, ![[#]](kuvat/msam10-c-4.gif) kompleksiluvut
kompleksiluvut
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Luvut Luvut  Reaaliluvut [ 1 2 3 4 5 6 7
] Reaaliluvut [ 1 2 3 4 5 6 7
]
ESITIEDOT: KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) murtoluvut, murtoluvut, ![[#]](kuvat/msam10-c-4.gif) lukujärjestelmät, lukujärjestelmät, ![[#]](kuvat/msam10-c-4.gif) kompleksiluvut kompleksiluvut
|
|
Desimaaliesityksen perusteella rationaaliluvut ja irrationaaliluvut voidaan karakterisoida seuraavasti: Jos desimaaliesitys on päättyvä tai jaksollinen, kyseessä on rationaaliluku; esimerkiksi
0.3478 = 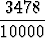 , 0.333... =
, 0.333... = 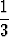 , 0.313131... =
, 0.313131... = 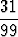 .
.
(Näistä viimeksi mainittu voidaan laskea geometrisen sarjan avulla.) Jos desimaaliesitys on päättymätön ja jaksoton, kyseessä on irrationaaliluku; esimerkiksi
 = 3.14159265358979323846264338327950288419716939937511... .
= 3.14159265358979323846264338327950288419716939937511... .
Reaaliluvun desimaaliesitys ei kaikissa tapauksissa ole yksikäsitteinen: 1 = 1.000... ja 0.999... ovat sama reaaliluku, kuten geometrisen sarjan avulla voidaan todeta.
![[#]](kuvat/msam10-c-4.gif) geometrinen sarja geometrinen sarja |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12