![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Lukujonon ja funktion raja-arvo
Lukujonon ja funktion raja-arvo  Sarjat [ 1
2 3 4 ]
Sarjat [ 1
2 3 4 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) summa ja tulo,
summa ja tulo, ![[#]](kuvat/msam10-c-4.gif) lukujonot,
lukujonot, ![[#]](kuvat/msam10-c-4.gif) lukujonon raja-arvo
lukujonon raja-arvo
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Neperin luku e,
Neperin luku e, ![[#]](kuvat/msam10-c-4.gif) luku
luku 
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Lukujonon ja funktion raja-arvo Lukujonon ja funktion raja-arvo  Sarjat [ 1
2 3 4 ] Sarjat [ 1
2 3 4 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) summa ja tulo, summa ja tulo, ![[#]](kuvat/msam10-c-4.gif) lukujonot, lukujonot, ![[#]](kuvat/msam10-c-4.gif) lukujonon raja-arvo lukujonon raja-arvo
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) Neperin luku e, Neperin luku e, ![[#]](kuvat/msam10-c-4.gif) luku luku 
|
|
Lähes ainoa sarjatyyppi, jonka suppeneminen ja summa voidaan alkeellisin keinoin selvittää on geometrinen sarja
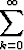 qk.
qk.
Tämän osasumma on geometrinen summa
sn = 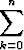 qk =
qk = 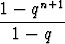 , jos q
, jos q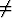 1.
1.
Jos q = 1, on sn = n + 1.
Jos |q| < 1, on osasummalla sn raja-arvo
s = limn
 sn =
sn = 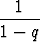 .
.
Jos q > 1, karkaavat osasummat äärettömyyteen. Jos q < -1, heilahtelevat osasummat mitään raja-arvoa lähestymättä.
Geometrinen sarja siis suppenee, jos ja vain jos |q| < 1. Tällöin sen summa on
s = 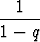 .
.
![[#]](kuvat/msam10-c-4.gif) geometrinen summa geometrinen summa![[#]](kuvat/msam10-c-4.gif) raja-arvo (lukujonon) raja-arvo (lukujonon) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12