![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Lukujonon ja funktion raja-arvo
Lukujonon ja funktion raja-arvo  Sarjat [ 1
2 3 4 ]
Sarjat [ 1
2 3 4 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) summa ja tulo,
summa ja tulo, ![[#]](kuvat/msam10-c-4.gif) lukujonot,
lukujonot, ![[#]](kuvat/msam10-c-4.gif) lukujonon raja-arvo
lukujonon raja-arvo
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Neperin luku e,
Neperin luku e, ![[#]](kuvat/msam10-c-4.gif) luku
luku 
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Lukujonon ja funktion raja-arvo Lukujonon ja funktion raja-arvo  Sarjat [ 1
2 3 4 ] Sarjat [ 1
2 3 4 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) summa ja tulo, summa ja tulo, ![[#]](kuvat/msam10-c-4.gif) lukujonot, lukujonot, ![[#]](kuvat/msam10-c-4.gif) lukujonon raja-arvo lukujonon raja-arvo
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) Neperin luku e, Neperin luku e, ![[#]](kuvat/msam10-c-4.gif) luku luku 
|
|
Sarjaa
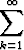
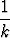
kutsutaan harmoniseksi sarjaksi. Sen osasummalle sn ei voida esittää lauseketta, mutta sarja voidaan päätellä hajaantuvaksi seuraavalla tavalla.
Koska kaikki harmonisen sarjan termit ovat positiivisia, on osasummien jono kasvava: s1 < s2 < s3 < s4 < .... Osasummalle, jonka indeksi on n = 2p, pätee seuraava:
| s2p | = | 1 + 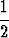 + + 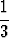 + + 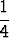 + + 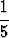 + ... + + ... + 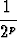 | ||
| = | 1 + 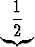 + + 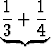 + + 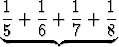 | |||
+ 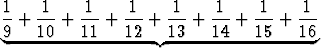 +... . +... . |
s2p > 1 + 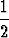 + 2 .
+ 2 . 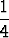 + 4 .
+ 4 . 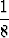 + 8 .
+ 8 . 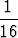 + ... + 2p-1 .
+ ... + 2p-1 .  = 1 +
= 1 + 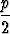 .
.
Antamalla p 
 saadaan
saadaan
limp
 s2p > limp
s2p > limp

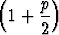 =
=  .
.
Sarja siis ilmeisestikin hajaantuu.
Huomattakoon, että harmonisen sarjan termit lähestyvät nollaa, ts.
limk

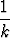 = 0,
= 0,
mutta siitä huolimatta sarja hajaantuu.
Esimerkki osoittaa, että sarjojen suppenemisen tutkiminen ja niiden summien määrittäminen ei ole aivan yksinkertaista.
![[#]](kuvat/msam10-c-4.gif) raja-arvo (lukujonon) raja-arvo (lukujonon) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12