![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Lukujonon ja funktion raja-arvo
Lukujonon ja funktion raja-arvo  Lukujonon
raja-arvo [ 1 2 3 4 5 6 7 ]
Lukujonon
raja-arvo [ 1 2 3 4 5 6 7 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) lukujonot
lukujonot
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) funktion raja-arvo,
funktion raja-arvo, ![[#]](kuvat/msam10-c-4.gif) Neperin luku e
Neperin luku e
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Lukujonon ja funktion raja-arvo Lukujonon ja funktion raja-arvo  Lukujonon
raja-arvo [ 1 2 3 4 5 6 7 ] Lukujonon
raja-arvo [ 1 2 3 4 5 6 7 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) lukujonot lukujonot
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) funktion raja-arvo, funktion raja-arvo, ![[#]](kuvat/msam10-c-4.gif) Neperin luku e Neperin luku e
|
|
Lukujonossa a1, a2, a3, ... (jossa on äärettömän monta termiä) voivat luvut lähestyä jotakin arvoa, kun jonossa edetään yhä pidemmälle. Tätä arvoa kutsutaan lukujonon raja-arvoksi ja merkitään
limn
 an.
an.
Esimerkkinä olkoon rekursiivisesti määritelty jono
a0 = 1, an+1 =  + an -
+ an -  a
a , n = 0, 1, 2, 3, ... ,
, n = 0, 1, 2, 3, ... ,
jonka termeillä on seuraavia arvoja:
| a0 | = 1.0, |
| a1 | = 1.25, |
| a2 | = 1.359375, |
| a3 | = 1.39739990234375, |
| a4 | = 1.409218280576169, |
| a5 | = 1.412744239998656, |
| a6 | = 1.413782668086311, |
| a7 | = 1.414087309940999, |
| a8 | = 1.414176579906956, |
| a9 | = 1.414202730117622, |
| a10 | = 1.414210389649588, |
| a11 | = 1.414212633101378, |
| a12 | = 1.414213290195495, |
| a13 | = 1.414213482654103, |
| a14 | = 1.414213539023941, |
| a15 | = 1.414213555534286, |
| a16 | = 1.414213560370054, |
| a17 | = 1.414213561786418, |
| a18 | = 1.414213562201261, |
| a19 | = 1.414213562322766, |
| a20 | = 1.414213562358354 |
Nämä näyttäisivät lähestyvän lukua 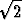
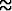 1.414213562373095. Itse asiassa näin
onkin.
1.414213562373095. Itse asiassa näin
onkin.
![[#]](kuvat/msam10-c-4.gif) rekursiivisesti määritelty lukujono rekursiivisesti määritelty lukujono |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12