![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Lukujonon ja funktion raja-arvo
Lukujonon ja funktion raja-arvo  Funktion
raja-arvo [ 1 2 3 4 5 6 ]
Funktion
raja-arvo [ 1 2 3 4 5 6 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot
reaalifunktiot
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) lukujonon raja-arvo,
lukujonon raja-arvo, ![[#]](kuvat/msam10-c-4.gif) funktion jatkuvuus
funktion jatkuvuus
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Lukujonon ja funktion raja-arvo Lukujonon ja funktion raja-arvo  Funktion
raja-arvo [ 1 2 3 4 5 6 ] Funktion
raja-arvo [ 1 2 3 4 5 6 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot reaalifunktiot
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) lukujonon raja-arvo, lukujonon raja-arvo, ![[#]](kuvat/msam10-c-4.gif) funktion jatkuvuus funktion jatkuvuus
|
|
Lauseke
f(x) = 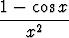
määrittelee reaalimuuttujan reaaliarvoisen funktion f, jonka lähtöjoukko muodostuu nollasta eroavista reaaliluvuista. Periaatteessa f(0) voidaan määritellä miten tahansa. Luontevaa kuitenkin on ensin tutkia, miten funktio f käyttäytyy, kun x on lähellä origoa.
Jos funktion arvot lähestyvät jotakin kiinteää arvoa, kun x lähestyy origoa, kyseistä arvoa sanotaan funktion raja-arvoksi origossa. Tällöin on myös luontevaa määritellä f(0) juuri täksi arvoksi (jolloin funktiosta f tulee jatkuva funktio).
Numeeriset kokeilut antavat seuraavat tulokset:
| x = ±0.5, | f(x) = 0.489669752; |
| x = ±0.05, | f(x) = 0.499895842; |
| x = ±0.005, | f(x) = 0.499998958; |
| x = ±0.0005, | f(x) = 0.499999989. |
Näyttäisi siis, että funktion raja-arvo origossa on = 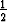 . (Numeerisissa kokeiluissa
on tosin oltava varovainen, koska pyöristysvirheet voivat yllättäen aiheuttaa jopa
täysin virheellisiä tuloksia.)
. (Numeerisissa kokeiluissa
on tosin oltava varovainen, koska pyöristysvirheet voivat yllättäen aiheuttaa jopa
täysin virheellisiä tuloksia.)
Esimerkin tapauksessa raja-arvo todellakin on = 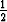 ja merkitään
ja merkitään
limx 0
0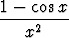 =
=  .
.
![[#]](kuvat/msam10-c-4.gif) funktio funktio![[#]](kuvat/msam10-c-4.gif) funktio (reaali-) funktio (reaali-)![[#]](kuvat/msam10-c-4.gif) lähtöjoukko lähtöjoukko![[#]](kuvat/msam10-c-4.gif) jatkuvuus jatkuvuus![[#]](kuvat/msam10-c-4.gif) pyöristysvirhe pyöristysvirhe |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12