![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Lukujonon ja funktion raja-arvo
Lukujonon ja funktion raja-arvo  Funktion
raja-arvo [ 1 2 3 4 5 6 ]
Funktion
raja-arvo [ 1 2 3 4 5 6 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot
reaalifunktiot
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) lukujonon raja-arvo,
lukujonon raja-arvo, ![[#]](kuvat/msam10-c-4.gif) funktion jatkuvuus
funktion jatkuvuus
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Lukujonon ja funktion raja-arvo Lukujonon ja funktion raja-arvo  Funktion
raja-arvo [ 1 2 3 4 5 6 ] Funktion
raja-arvo [ 1 2 3 4 5 6 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot reaalifunktiot
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) lukujonon raja-arvo, lukujonon raja-arvo, ![[#]](kuvat/msam10-c-4.gif) funktion jatkuvuus funktion jatkuvuus
|
|
Yleisesti reaalifunktion raja-arvon käsite määritellään seuraavalla tavalla:
Jotta funktion f raja-arvo pisteessä a olisi b (merkitään limx af(x) = b), on
tilanteen oltava sellainen, että asetetaanpa miten tiukka etäisyysvaatimus
tahansa, funktion arvot ovat tätä etäisyyttä lähempänä arvoa b, kun muuttuja x
rajoitetaan riittävän lähelle tarkastelukohtaa a.
af(x) = b), on
tilanteen oltava sellainen, että asetetaanpa miten tiukka etäisyysvaatimus
tahansa, funktion arvot ovat tätä etäisyyttä lähempänä arvoa b, kun muuttuja x
rajoitetaan riittävän lähelle tarkastelukohtaa a.
Mitä tiukempi etäisyysvaatimus on, sitä pienempään pisteen a ympäristöön muuttuja x on yleensä rajoitettava. Jokaista positiivista etäisyyskynnystä vastaa kuitenkin aina jokin, ehkä hyvinkin pieni alue pisteen a ympärillä, jossa vaatimus toteutuu. Funktion arvosta pisteessä a ei tällöin vaadita mitään; funktion ei tarvitse edes olla tässä pisteessä määritelty.
Täsmällisemmin lausuttuna edellä oleva voidaan ilmaista seuraavasti:
Funktion f raja-arvo pisteessä a on b, jos jokaista etäisyyskynnystä  (> 0)
kohden on olemassa pisteen a ympäristöä rajaava luku
(> 0)
kohden on olemassa pisteen a ympäristöä rajaava luku 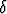 (myös > 0) siten, että
|f(x) - b| <
(myös > 0) siten, että
|f(x) - b| <  , kun |x - a| <
, kun |x - a| < 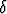 ja x
ja x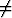 a. Itseisarvolausekkeet |x - a| ja
|f(x) - b| on syytä mieltää lukujen x ja a, vastaavasti f(x) ja b välisiksi
etäisyyksiksi.
a. Itseisarvolausekkeet |x - a| ja
|f(x) - b| on syytä mieltää lukujen x ja a, vastaavasti f(x) ja b välisiksi
etäisyyksiksi.
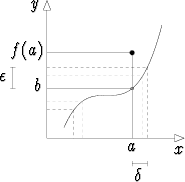
![[#]](kuvat/msam10-c-4.gif) funktio (reaali-) funktio (reaali-)![[#]](kuvat/msam10-c-4.gif) itseisarvo (reaaliluvun) itseisarvo (reaaliluvun) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12