![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Lukujonon ja funktion raja-arvo
Lukujonon ja funktion raja-arvo  Funktion
raja-arvo [ 1 2 3 4 5 6 ]
Funktion
raja-arvo [ 1 2 3 4 5 6 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot
reaalifunktiot
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) lukujonon raja-arvo,
lukujonon raja-arvo, ![[#]](kuvat/msam10-c-4.gif) funktion jatkuvuus
funktion jatkuvuus
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Lukujonon ja funktion raja-arvo Lukujonon ja funktion raja-arvo  Funktion
raja-arvo [ 1 2 3 4 5 6 ] Funktion
raja-arvo [ 1 2 3 4 5 6 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot reaalifunktiot
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) lukujonon raja-arvo, lukujonon raja-arvo, ![[#]](kuvat/msam10-c-4.gif) funktion jatkuvuus funktion jatkuvuus
|
|
 ja raja-arvo
äärettömyydessä
ja raja-arvo
äärettömyydessä
Funktio saattaa käyttäytyä myös siten, että muuttujan x lähestyessä kohtaa a sen arvot lähestyvät eri arvoja riippuen siitä kummalta puolen x lähestyy arvoa a. Tällaisessa tilanteessa puhutaan funktion oikeanpuolisesta ja vasemmanpuolisesta raja-arvosta. Näitä merkitään
limx a+f(x) ja limx
a+f(x) ja limx a-f(x),
a-f(x),
jolloin luvun a perässä oleva plusmerkki tarkoittaa oikeanpuolista, miinusmerkki vasemmanpuolista lähestymistä.
Esimerkki tällaisesta funktiosta on arctan(1/x) origossa, jolle
limx 0+ arctan(1/x) =
0+ arctan(1/x) = 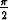 ja limx
ja limx 0- arctan(1/x) = -
0- arctan(1/x) = -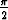 .
.
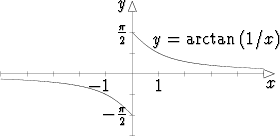
Funktion raja-arvoa voidaan tarkastella myös, kun muuttuja x lähestyy ääretöntä positiivisessa tai negatiivisessa suunnassa. Tällöin merkitään
limx -
- f(x) = b tai limx
f(x) = b tai limx
 f(x) = b.
f(x) = b.
Missä tahansa rajaprosessissa funktion arvot voivat myös lähestyä positiivista tai negatiivista ääretöntä (jolloin raja-arvon ei sanota olevan olemassa, koska se ei ole (äärellinen) reaaliluku). Merkinnät ovat ilmeiset:
limx a-f(x) =
a-f(x) =  , limx
, limx
 f(x) = -
f(x) = - , jne.
, jne.
![[#]](kuvat/msam10-c-4.gif) arcus-funktio arcus-funktio |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12