![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Lukujonon ja funktion raja-arvo
Lukujonon ja funktion raja-arvo  Funktion
raja-arvo [ 1 2 3 4 5 6 ]
Funktion
raja-arvo [ 1 2 3 4 5 6 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot
reaalifunktiot
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) lukujonon raja-arvo,
lukujonon raja-arvo, ![[#]](kuvat/msam10-c-4.gif) funktion jatkuvuus
funktion jatkuvuus
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Lukujonon ja funktion raja-arvo Lukujonon ja funktion raja-arvo  Funktion
raja-arvo [ 1 2 3 4 5 6 ] Funktion
raja-arvo [ 1 2 3 4 5 6 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot reaalifunktiot
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) lukujonon raja-arvo, lukujonon raja-arvo, ![[#]](kuvat/msam10-c-4.gif) funktion jatkuvuus funktion jatkuvuus
|
|
Seuraavista raja-arvoista kolme ensimmäistä muodostavat pohjan kyseessä olevien alkeisfunktioiden derivaattojen johtamiselle. Neljäs osoittaa, että eksponenttifunktio kasvaa nopeammin kuin mikä tahansa muuttujan potenssi.
limx 0 0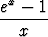 = 1; = 1; |
limx 0 0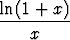 = 1; = 1; |
limx 0 0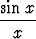 = 1; = 1; |
limx  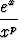 = =  , p luonnollinen luku. , p luonnollinen luku. |
Kolmannessa, siniä koskevassa kaavassa on argumentin oltava radiaaneissa. Raja-arvo voidaan tietenkin laskea myös siten, että x lausutaan asteissa; tällöin se ei kuitenkaan ole 1.
Ensimmäinen kaava johtaa siihen, että eksponenttifunktion derivaatta on se itse (ks. alkeisfunktioiden derivointia). Kaava puolestaan on seuraus Neperin luvun määritelmästä, kuten seuraava osoittaa.
Merkitsemällä t = 1/x saadaan
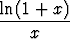 = t ln
= t ln 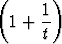 = ln
= ln 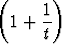 t.
t.
Jos x  0, niin t
0, niin t  ±
± . Neperin luvun määritelmästä seuraa, että
limt
. Neperin luvun määritelmästä seuraa, että
limt
 (1 + 1/t)t = e; pieni lisäpäättely osoittaa, että näin on myös, jos t
(1 + 1/t)t = e; pieni lisäpäättely osoittaa, että näin on myös, jos t  -
- .
Eo. lausekkeen raja-arvo on siis ln e = 1, kun x
.
Eo. lausekkeen raja-arvo on siis ln e = 1, kun x  0, ja toinen kaava on
todistettu.
0, ja toinen kaava on
todistettu.
Ensimmäinen kaava voidaan palauttaa tähän merkitsemällä y = ex - 1 eli
x = ln(1 + y), jolloin x  0, jos ja vain jos y
0, jos ja vain jos y  0. Tällöin
0. Tällöin
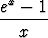 =
= 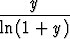 -
- 1.
1.
Huomattakoon, että eo. päättelyissä nojaudutaan tietoon eksponentti- ja
logaritmifunktioiden jatkuvuudesta: Esimerkiksi tiedosta (1 + 1/t)t  e seuraa
ln[(1 + 1/t)t]
e seuraa
ln[(1 + 1/t)t]  ln e vain, jos logaritmifunktio tiedetään jatkuvaksi pisteessä
e.
ln e vain, jos logaritmifunktio tiedetään jatkuvaksi pisteessä
e.
Kolmannen ja neljännen kaavan johtoa ei tässä lähemmin käsitellä.
![[#]](kuvat/msam10-c-4.gif) raja-arvo
(standardi-, lukujonon) raja-arvo
(standardi-, lukujonon)![[#]](kuvat/msam10-c-4.gif) derivointi (alkeisfunktioiden) derivointi (alkeisfunktioiden)![[#]](kuvat/msam10-c-4.gif) eksponenttifunktio eksponenttifunktio![[#]](kuvat/msam10-c-4.gif) logaritmifunktio logaritmifunktio![[#]](kuvat/msam10-c-4.gif) potenssifunktio potenssifunktio![[#]](kuvat/msam10-c-4.gif) sini sini![[#]](kuvat/msam10-c-4.gif) radiaani radiaani![[#]](kuvat/msam10-c-4.gif) aste aste![[#]](kuvat/msam10-c-4.gif) Neperin luku Neperin luku![[#]](kuvat/msam10-c-4.gif) jatkuvuus jatkuvuus |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12