![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Alkeisfunktiot
Alkeisfunktiot  Logaritmifunktio [ 1 2 3
4 ]
Logaritmifunktio [ 1 2 3
4 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot,
reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) eksponenttifunktio
eksponenttifunktio
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Alkeisfunktiot Alkeisfunktiot  Logaritmifunktio [ 1 2 3
4 ] Logaritmifunktio [ 1 2 3
4 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot, reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) eksponenttifunktio eksponenttifunktio
KATSO MYÖS: |
|
Eksponenttifunktio expa(x) = ax, missä a > 1, on määritelty kaikilla
reaaliarvoilla x, on aidosti kasvava ja saa arvoikseen kaikki positiiviset reaaliarvot.
Tällöin kyseessä on bijektio 

 + ja sillä on käänteisfunktio
+ ja sillä on käänteisfunktio  +
+ 
 .
(
.
( + = positiiviset reaaliluvut.)
+ = positiiviset reaaliluvut.)
Käänteisfunktiota kutsutaan a-kantaiseksi logaritmiksi ja merkitään loga. Siis
y = expa(x) = ax 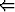
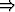 x = logay.
x = logay.
Jos erityisesti kantalukuna on Neperin luku e, puhutaan luonnollisesta logaritmista, jota merkitään ln. Jos kantalukuna on 10, kyseessä on Briggsin logaritmi merkintänä yleensä lg.
Vastaava päättely kuin edellä voidaan tehdä myös tapauksessa 0 < a < 1. Ainoana erona on, että eksponenttifunktio expa ei tällöin ole aidosti kasvava vaan vähenevä. Tällaisia logaritmifunktioita ei kuitenkaan yleensä käytetä.
Jos a > 1, on logaritmifunktio aidosti kasvava; jos 0 < a < 1, niin aidosti vähenevä.
Koska a0 = 1 ja a1 = a, on kantaluvusta a riippumatta
loga1 = 0 ja logaa = 1,
ts. ’ykkösen logaritmi on nolla’ ja ’kantaluvun logaritmi on yksi’.
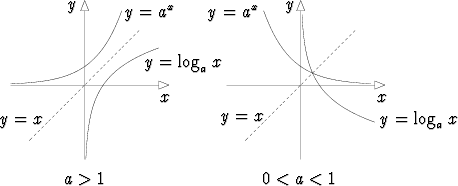
![[#]](kuvat/msam10-c-4.gif) funktio funktio![[#]](kuvat/msam10-c-4.gif) eksponenttifunktio eksponenttifunktio![[#]](kuvat/msam10-c-4.gif) kasvava (funktio) kasvava (funktio)![[#]](kuvat/msam10-c-4.gif) kasvava (funktio) kasvava (funktio)![[#]](kuvat/msam10-c-4.gif) bijektio bijektio![[#]](kuvat/msam10-c-4.gif) käänteisfunktio käänteisfunktio![[#]](kuvat/msam10-c-4.gif) käänteisfunktio käänteisfunktio![[#]](kuvat/msam10-c-4.gif) Neperin luku Neperin luku![[#]](kuvat/msam10-c-4.gif) vähenevä (funktio) vähenevä (funktio)![[#]](kuvat/msam10-c-4.gif) vähenevä (funktio) vähenevä (funktio) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12