![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Alkeisfunktiot
Alkeisfunktiot  Logaritmifunktio [ 1 2 3
4 ]
Logaritmifunktio [ 1 2 3
4 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot,
reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) eksponenttifunktio
eksponenttifunktio
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Alkeisfunktiot Alkeisfunktiot  Logaritmifunktio [ 1 2 3
4 ] Logaritmifunktio [ 1 2 3
4 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot, reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) eksponenttifunktio eksponenttifunktio
KATSO MYÖS: |
|
Olkoon y1 = ax1, y2 = ax2 ja y = ax. Tällöin on x1 = logay1, x2 = logay2 ja x = logay. Eksponenttifunktion laskusäännöt
ax1 ax2 = ax1+x2 ja (ax)b = abx
saavat tällöin muodon y1y2 = alogay1+logay2 ja yb = ab logay. Muodostamalla kummastakin puolesta a-kantainen logaritmi saadaan logaritmin laskusäännöt:
loga(y1y2) = logay1 + logay2 ja loga(yb) = b logay.
Yhdistämällä säännöt saadaan osamäärän logaritmille
loga(y1/y2) = loga(y1y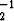 ) = logay1 - logay2.
) = logay1 - logay2.
Mikä tahansa logaritmi on helposti palautettavissa luonnolliseen logaritmiin.
Koska eksponenttifunktio ja logaritmifunktio ovat käänteisfunktioita, on
alogax = x, mistä saadaan ottamalla luonnollinen logaritmi kummastakin
puolesta
(logax)(ln a) = ln x. Siis
logax = 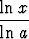 .
.
![[#]](kuvat/msam10-c-4.gif) laskusääntö (eksponenttifunktion) laskusääntö (eksponenttifunktion)![[#]](kuvat/msam10-c-4.gif) käänteisfunktio käänteisfunktio![[#]](kuvat/msam10-c-4.gif) käänteisfunktio käänteisfunktio |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12