![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Alkeisfunktiot
Alkeisfunktiot  Eksponenttifunktio [ 1 2
3 ]
Eksponenttifunktio [ 1 2
3 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot,
reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) potenssi
potenssi
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) logaritmifunktio
logaritmifunktio
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Alkeisfunktiot Alkeisfunktiot  Eksponenttifunktio [ 1 2
3 ] Eksponenttifunktio [ 1 2
3 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot, reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) potenssi potenssi
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) logaritmifunktio logaritmifunktio
|
|
Yleinen eksponenttifunktio expa : 

 määritellään asettamalla
määritellään asettamalla
expa(x) = ax.
Luku a on eksponenttifunktion kantaluku, jonka tulee olla > 0, koska potenssi ei muutoin ole — ongelmitta — määritelty kaikilla reaalisilla eksponenteilla x. Tapaus a = 1 antaa vakiofunktion (= 1) eikä ole mielenkiintoinen.
Usein eksponenttifunktiolla tarkoitetaan tapausta, jossa kantalukuna on Neperin
luku e 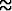 2.71828. Tällöin merkitään ex = exp(x).
2.71828. Tällöin merkitään ex = exp(x).
Eksponenttifunktion tärkeimmät ominaisuudet ovat seuraavat:
| ax1ax2 = ax1+x2 eli expa(x1) expa(x2) = expa(x1 + x2), |
| (ax)y = axy eli (expa(x))y = expa(xy). |
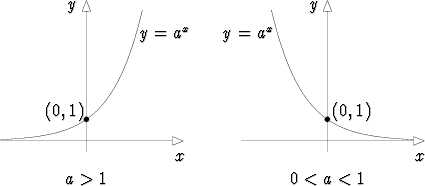
![[#]](kuvat/msam10-c-4.gif) funktio funktio![[#]](kuvat/msam10-c-4.gif) potenssi (kokonaisluku-) potenssi (kokonaisluku-)![[#]](kuvat/msam10-c-4.gif) potenssi (murto-) potenssi (murto-)![[#]](kuvat/msam10-c-4.gif) potenssi (irrationaali-) potenssi (irrationaali-)![[#]](kuvat/msam10-c-4.gif) potenssi (kompleksinen) potenssi (kompleksinen)![[#]](kuvat/msam10-c-4.gif) Neperin luku Neperin luku![[#]](kuvat/msam10-c-4.gif) kasvava (funktio) kasvava (funktio)![[#]](kuvat/msam10-c-4.gif) kasvava (funktio) kasvava (funktio)![[#]](kuvat/msam10-c-4.gif) vähenevä (funktio) vähenevä (funktio)![[#]](kuvat/msam10-c-4.gif) vähenevä (funktio) vähenevä (funktio) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12