![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Alkeisfunktiot
Alkeisfunktiot  Eksponenttifunktio [ 1 2
3 ]
Eksponenttifunktio [ 1 2
3 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot,
reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) potenssi
potenssi
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) logaritmifunktio
logaritmifunktio
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Alkeisfunktiot Alkeisfunktiot  Eksponenttifunktio [ 1 2
3 ] Eksponenttifunktio [ 1 2
3 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot, reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) potenssi potenssi
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) logaritmifunktio logaritmifunktio
|
|
Eksponenttifunktion y = ekx merkitys sovelluksissa perustuu paljolti siihen, että se toteuttaa differentiaaliyhtälön
y' = ky.
Monia ilmiöitä voidaan nimittäin kuvata tämäntyyppisellä differentiaaliyhtälöllä. Differentiaaliyhtälöä sanotaan ilmiön matemaattiseksi malliksi.
Olkoon esimerkiksi p(t) funktio, joka esittää väestön suuruutta ajanhetkellä t.
Voidaan ajatella, että väestön lisäys  p lyhyellä aikavälillä
p lyhyellä aikavälillä  t on suoraan
verrannollinen olemassaolevan väestön määrään ja aikavälin pituuteen:
t on suoraan
verrannollinen olemassaolevan väestön määrään ja aikavälin pituuteen:
 p = kp
p = kp t, missä k on positiivinen verrannollisuuskerroin. Jakamalla aikavälin
pituudella
t, missä k on positiivinen verrannollisuuskerroin. Jakamalla aikavälin
pituudella  t saadaan
t saadaan
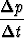 = kp.
= kp.
Koska  p = p(t +
p = p(t +  t) - p(t), on vasen puoli väestön suuruutta ajanhetkellä t
kuvaavan funktion p(t) erotusosamäärä, jolloin saadaan differentiaaliyhtälö
t) - p(t), on vasen puoli väestön suuruutta ajanhetkellä t
kuvaavan funktion p(t) erotusosamäärä, jolloin saadaan differentiaaliyhtälö
p'(t) = kp(t) eli p' = kp,
kun  t
t  0. Tämä on differentiaaliyhtälö, jonka ratkaisuna on eksponenttifunktio
p(t) = Cekt; tässä C on mikä tahansa vakio.
0. Tämä on differentiaaliyhtälö, jonka ratkaisuna on eksponenttifunktio
p(t) = Cekt; tässä C on mikä tahansa vakio.
Eo. differentiaaliyhtälöä kutsutaan väestönkasvun eksponentiaaliseksi malliksi. Sellaisena se on luonnollisesti äärimmäisen yksinkertainen, koska esimerkiksi kuolleisuuteen ei ole kiinnitetty mitään huomiota, ei myöskään populaation kasvaessa yhä rajallisemmiksi muuttuviin ympäristöresursseihin kuten saatavilla olevaan ravintoon yms.
Samantyyppiseen malliin päästään tarkasteltaessa aineen radioaktiivista
hajoamista. Hajoavien atomien määrä  m on suoraan verrannollinen aineen
määrään kyseisellä hetkellä m(t) ja tarkasteltavan aikavälin pituuteen
m on suoraan verrannollinen aineen
määrään kyseisellä hetkellä m(t) ja tarkasteltavan aikavälin pituuteen  t. Siis:
t. Siis:
 m = -km
m = -km t. Miinusmerkki aiheutuu siitä, että
t. Miinusmerkki aiheutuu siitä, että  m merkitsee aineen
vähenemistä ja on siis negatiivinen; kerroin k oletetaan positiiviseksi.
m merkitsee aineen
vähenemistä ja on siis negatiivinen; kerroin k oletetaan positiiviseksi.
Samaan tapaan kuin edellä tästä päädytään differentiaaliyhtälöön m' = -km, jonka ratkaisu on m = Ce-kt. Tässä C on vakio, joka riippuu ainemäärästä tarkastelun alkuhetkellä. Verrannollisuuskerroin k on aineelle ominainen vakio (vastaten puoliintumisaikaa).
![[#]](kuvat/msam10-c-4.gif) differentiaaliyhtälö differentiaaliyhtälö![[#]](kuvat/msam10-c-4.gif) erotusosamäärä erotusosamäärä![[#]](kuvat/msam10-c-4.gif) derivaatta derivaatta |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12