Sisällön pääryhmät Derivaatta Differentiaaliyhtälöt [ 1 2 3 ] ESITIEDOT:  derivaatta KATSO MYÖS:  derivointisäännöt,  alkeisfunktioiden derivaatat

Kansisivu  Sisältö  Hakemisto

Differentiaaliyhtälöksi kutsutaan yhtälöä, jossa tuntemattomana on funktio ja joka sisältää tuntemattoman funktion derivaattoja. Esimerkiksi y'' + y = 0 on differentiaaliyhtälö. Tuntemattomana on tällöin funktio y = y(x). Yhtälön ratkaisu on

y = C₁ sin x + C₂ cos x,

missä C₁ ja C₂ ovat mielivaltaisia vakioita. Ratkaisu ei siten ole yksikäsitteinen, vaan vakioille voidaan antaa mitkä arvot tahansa. Että eo. lauseke todella on ratkaisu, nähdään derivoimalla: Koska

y' = C₁ cos x - C₂ sin x, y'' = -C₁ sin x - C₂ cos x,

on todellakin y'' + y = 0 kaikilla muuttujan x arvoilla.

Toisena esimerkkinä olkoon differentiaaliyhtälö x²y' + (xy - 2)² = 0, jonka ratkaisu on

y = .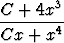

Tässä C on jälleen vapaasti valittava vakio.

Jotta saataisiin yksikäsitteinen ratkaisu, tarvitaan differentiaaliyhtälön ohella jokin lisäehto. Edellisen esimerkin tapauksessa tällainen olisi vaikkapa y(0) = 0, y'(0) = 1, jolloin ainoa mahdollinen ratkaisu on y = sin x, ts. C₁ = 1, C₂ = 0.

Jälkimmäisessä esimerkissä vakioita on vain yksi, jolloin tarvitaan vain yksi lisävaatimus. Esimerkiksi y(1) = 2 antaisi C = 2.

Lisäehtoa, jossa annetaan funktion ja sen riittävän monen derivaatan arvot tietyllä argumentin arvolla, kutsutaan nimellä alkuehto.

Differentiaaliyhtälöiden ratkaisemiseksi on melkoinen määrä erilaisia menettelyjä, joita ei tässä lähemmin tarkastella. Läheskään aina ei yhtälön ratkaiseminen tavallisten alkeisfunktioiden avulla ole edes mahdollista.

Differentiaaliyhtälöiden merkitys perustuu siihen, että niiden avulla voidaan kuvata erilaisia luonnon ja tekniikan ilmiöitä. Ratkaisemalla yhtälö saadaan tietoa ilmiön käyttäytymisestä.

yhtälö  funktio  derivaatta  derivaatta (toinen)  derivointi (alkeisfunktioiden)  alkeisfunktio

Kivelä, niinkuin matematiikka, versio 1.12