Sisällön pääryhmät Derivaatta Differentiaaliyhtälöt [ 1 2 3 ] ESITIEDOT:  derivaatta KATSO MYÖS:  derivointisäännöt,  alkeisfunktioiden derivaatat

Kansisivu  Sisältö  Hakemisto

Tarkastellaan kappaletta, joka riippuu kiinteästä tuesta kierrejousen varassa ja joka voidaan saattaa pystysuoraan liikkeeseen. Poikkeama tasapainoasemasta olkoon ajan funktio y(t). Se olkoon positiivinen tasapainoaseman yläpuolella, negatiivinen alapuolella.

Jos kappaletta nostetaan ylöspäin, puristuu kierrejousi kokoon ja työntää kappaletta alaspäin. Jos sitä vedetään alaspäin, venyy kierrejousi ja vetää ylöspäin. Jousen aiheuttama voima F₁ on verrannollinen poikkeamaan tasapainoasemasta: F₁ = -ky, missä k on positiivinen vakio. Etumerkki aiheutuu siitä, että voiman suunta on vastakkainen poikkeamalle.

Oletetaan lisäksi, että kappaleen alapuolelle on sijoitettu nesteellä täytetty astia siten, että kappaleen liike tapahtuu nesteen sisällä. Tällöin neste vaimentaa kappaleen liikettä. Vaimentava voima F₂ on sitä suurempi, mitä nopeammin kappale liikkuu; voiman suunta on nopeudelle y' vastakkainen: F₂ = -cy', missä verrannollisuuskerroin c on positiivinen vakio.

Sysättynä pystysuoraan liikkeeseen kappale alkaa heilahdella nesteen vaimentaessa heilahtelua. Poikkeama y(t) voidaan laskea seuraavasti:

Newtonin lain mukaan kappaleeseen vaikuttava kokonaisvoima on kappaleen massan ja kiihtyvyyden tulo: F = my''. Kappaleen pystysuora heilahtelu voidaan tällöin mallintaa differentiaaliyhtälöllä, jonka molemmat puolet esittävät kappaleeseen vaikuttavaa voimaa: F = F₁ + F₂ eli my'' = -ky - cy'.

Jos kappale sysätään liikkeelle (ajanhetkellä t = 0) siten, että sille tasapainoasemassa annetaan alkunopeus v₀ ylöspäin, on differentiaaliyhtälö ratkaistava alkuehtona y(0) = 0, y'(0) = v₀. Ratkaisuna on tällöin

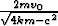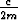y(t) =  e^{- t}  sin ,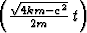

missä on oletettu, että nesteen aiheuttama vaimennus on vähäistä: c < 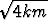. Ratkaisun laskemista ei tässä tarkastella.

funktio  nopeus  derivaatta  Newton  kiihtyvyys  derivaatta (toinen)  eksponenttifunktio  sini

Kivelä, niinkuin matematiikka, versio 1.12