Sisällön pääryhmät Derivaatta Derivointisäännöt [ 1 2 3 4 ] ESITIEDOT:  derivaatta KATSO MYÖS:  alkeisfunktioiden derivaatat

Kansisivu  Sisältö  Hakemisto

Summan derivaatta lasketaan termeittäin:

D[f(x) + g(x)] = f'(x) + g'(x).

Vakiokerrannaisen derivaatta: Jos c on vakio, se voidaan siirtää derivointioperaattorin D eteen:

D[cf(x)] = cf'(x).

Tulon derivaatta: ’Edellisen tekijän derivaatta kertaa jälkimmäinen plus edellinen kertaa jälkimmäisen derivaatta’:

D[f(x)g(x)] = f'(x)g(x) + f(x)g'(x).

Useamman tekijän tuloihin tämä yleistyy seuraavaan tapaan:

D[f(x)g(x)h(x)] = f'(x)g(x)h(x) + f(x)g'(x)h(x) + f(x)g(x)h'(x).

Osamäärän derivaatta: ’Osoittajan derivaatta kertaa nimittäjä miinus osoittaja kertaa nimittäjän derivaatta per nimittäjä toiseen’:

D[f(x)/g(x)] = .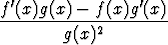

Kaikki säännöt voidaan johtaa suoraan derivaatan määritelmän pohjalta erotusosamäärän raja-arvona.

derivaatta  erotusosamäärä  raja-arvo (funktion)

Kivelä, niinkuin matematiikka, versio 1.12