![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Derivaatta
Derivaatta  Derivointisäännöt [ 1 2 3 4
]
Derivointisäännöt [ 1 2 3 4
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) derivaatta
derivaatta
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) alkeisfunktioiden derivaatat
alkeisfunktioiden derivaatat
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Derivaatta Derivaatta  Derivointisäännöt [ 1 2 3 4
] Derivointisäännöt [ 1 2 3 4
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) derivaatta derivaatta
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) alkeisfunktioiden derivaatat alkeisfunktioiden derivaatat
|
|
Implisiittinen derivointi on yhdistetyn funktion derivoimissäännön sovellus tapaukseen, missä funktiota ei ole annettu suoraan, vaan se tunnetaan yhtälönä, jonka argumentin arvot x ja funktion arvot y toteuttavat, esimerkiksi x4 + y4 = 2xy5. Jos löytyy pisteitä (x, y), jotka toteuttavat yhtälön, voidaan periaatteessa ratkaista y muuttujan x funktiona: y = y(x). Käytännössä ei välttämättä ole helppoa tai edes mahdollista löytää tälle funktiolle yksinkertaista lauseketta.
Jos funktio y(x) on olemassa, se toteuttaa siis yhtälön
x4 + y(x)4 = 2xy(x)5.
Jos voidaan olettaa, että funktio y on derivoituva, derivoidaan em. yhtälön molemmat puolet muuttujan x suhteen mm. yhdistetyn funktion derivoimissääntöä käyttäen:
4x3 + 4y(x)3y'(x) = 2y(x)5 + 10xy(x)4y'(x).
Tästä voidaan ratkaista y'(x):
y'(x) = 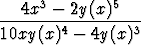 =
= 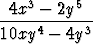 .
.
Tulos sisältää kuitenkin edelleen tuntemattoman lausekkeen y(x). Jos kuitenkin tiedetään arvopari (x, y), joka toteuttaa alkuperäisen yhtälön, saadaan funktion derivaatta tässä pisteessä. Esimerkkitapauksessa piste (1, 1) on käyrällä, jolloin siis y(1) = 1. Vastaava derivaatta on
y'(1) = 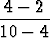 =
=  .
.
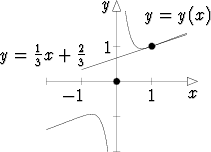
Funktion y derivoituvuus ei aina ole itsestään selvää. Esimerkiksi eo. yhtälö toteutuu myös origossa, jolloin siis on y(0) = 0. Tämä on kuitenkin funktion epäjatkuvuuspiste eikä derivaattakaan voi tällöin olla olemassa.
![[#]](kuvat/msam10-c-4.gif) yhdistetty
funktio yhdistetty
funktio![[#]](kuvat/msam10-c-4.gif) yhtälö yhtälö![[#]](kuvat/msam10-c-4.gif) derivoituvuus derivoituvuus![[#]](kuvat/msam10-c-4.gif) käyrä (taso-) käyrä (taso-) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12