![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Derivaatta
Derivaatta  Derivaatta [ 1 2 3 4 5 6
]
Derivaatta [ 1 2 3 4 5 6
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot,
reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) funktion raja-arvo
funktion raja-arvo
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) derivointisäännöt,
derivointisäännöt, ![[#]](kuvat/msam10-c-4.gif) alkeisfunktioiden derivaatat
alkeisfunktioiden derivaatat
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Derivaatta Derivaatta  Derivaatta [ 1 2 3 4 5 6
] Derivaatta [ 1 2 3 4 5 6
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot, reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) funktion raja-arvo funktion raja-arvo
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt, derivointisäännöt, ![[#]](kuvat/msam10-c-4.gif) alkeisfunktioiden derivaatat alkeisfunktioiden derivaatat
|
|
Derivaatta, so. erotusosamäärän raja-arvo ei välttämättä ole olemassa. Jos se on, funktiota sanotaan derivoituvaksi kyseisessä pisteessä x.
Esimerkkejä funktioista, jotka jossakin pisteessä eivät ole derivoituvia, ovat a) f(x) = |x| origossa ja b) f(x) = x sin(1/x) samoin origossa (missä määritellään f(0) = 0). Edellisen kuvaajalla on origossa kärki, jälkimmäisen käyttäytyminen on paljon monimutkaisempaa:
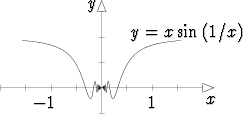
Funktion määritelmä on siinä määrin yleinen, että on helppoa muodostaa myös funktioita, jotka eivät ole missään derivoituvia tai ovat derivoituvia vain muutamissa pisteissä. Esimerkiksi määrittelemällä f(x) = x2, jos x on rationaalinen, ja f(x) = -x2, jos x on irrationaalinen, saadaan funktio, joka on derivoituva vain origossa.
![[#]](kuvat/msam10-c-4.gif) raja-arvo (funktion) raja-arvo (funktion)![[#]](kuvat/msam10-c-4.gif) kuvaaja kuvaaja![[#]](kuvat/msam10-c-4.gif) rationaaliluku rationaaliluku![[#]](kuvat/msam10-c-4.gif) irrationaaliluku irrationaaliluku |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12