Sisällön pääryhmät Derivaatta Derivaatta [ 1 2 3 4 5 6 ] ESITIEDOT:  reaalifunktiot,  funktion raja-arvo KATSO MYÖS:  derivointisäännöt,  alkeisfunktioiden derivaatat

Kansisivu  Sisältö  Hakemisto

Jos funktio f on jollakin tarkasteluvälillä derivoituva välin jokaisessa pisteessä, tulee tällä välillä määritellyksi derivaattafunktio f'(x). Jos tämä on derivoituva välin pisteessä x, saadaan alkuperäisen funktion toinen derivaatta eli toisen kertaluvun derivatta:

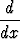f'(x) = f''(x) = D²f(x) = ,

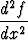missä kolme viimeksi mainittua ovat tavallisimmat tavat toisen derivaatan merkitsemiseen.

Jos funktio f''(x) saadaan määritellyksi jollakin välillä, voidaan jatkaa samaan tapaan ja saadaan korkeampien kertalukujen derivaatat f'''(x), f''''(x), jne.

Jos derivaatan kertaluku on kovin suuri, sitä ei enää ole mukavaa merkitä yläpilkuilla. Vaihtoehtoinen merkintätapa on käyttää sulkuihin pantua yläindeksiä, esimerkiksi f''''(x) = f⁽⁴⁾(x).

funktio

Kivelä, niinkuin matematiikka, versio 1.12