![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Derivaatta
Derivaatta  Derivointisäännöt [ 1 2 3 4
]
Derivointisäännöt [ 1 2 3 4
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) derivaatta
derivaatta
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) alkeisfunktioiden derivaatat
alkeisfunktioiden derivaatat
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Derivaatta Derivaatta  Derivointisäännöt [ 1 2 3 4
] Derivointisäännöt [ 1 2 3 4
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) derivaatta derivaatta
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) alkeisfunktioiden derivaatat alkeisfunktioiden derivaatat
|
|
Jos funktiot f ja g ovat toistensa käänteisfunktioita, on g(f(x)) = x. Mikäli kumpikin funktio on derivoituva, voidaan yhtälö derivoida puolittain yhdistetyn funktion derivoimissääntöä käyttäen, jolloin saadaan g'(f(x))f'(x) = 1 eli
f'(x) = 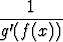 .
.
Funktion f derivaatta on siis saatu lausutuksi käänteisfunktion g derivaatan avulla. Kaava kirjoitetaan usein muotoon f'(x) = 1/g'(y), jolloin on merkitty y = f(x).
Tulos on käyttökelpoinen monien alkeisfunktioiden derivaattojen johtamisessa sekä lisäksi tapauksissa, missä käänteisfunktion lauseketta ei voida lausua alkeisfunktioiden avulla.
Esimerkiksi funktiolla
g(x) = 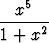
on käänteisfunktio f, mutta tätä ei voida esittää alkeisfunktioiden avulla. Koska
g(2) = 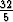 , on f(
, on f(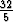 ) = 2. Käänteisfunktion derivoimiskaavan mukaisesti on
tällöin
) = 2. Käänteisfunktion derivoimiskaavan mukaisesti on
tällöin
f'(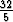 ) =
) = 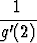 =
= 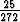 .
.
![[#]](kuvat/msam10-c-4.gif) käänteisfunktio käänteisfunktio![[#]](kuvat/msam10-c-4.gif) käänteisfunktio käänteisfunktio![[#]](kuvat/msam10-c-4.gif) derivoituvuus derivoituvuus![[#]](kuvat/msam10-c-4.gif) derivointi (alkeisfunktioiden) derivointi (alkeisfunktioiden)![[#]](kuvat/msam10-c-4.gif) alkeisfunktio alkeisfunktio |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12