Sisällön pääryhmät Derivaatta Differentiaaliyhtälöt [ 1 2 3 ] ESITIEDOT:  derivaatta KATSO MYÖS:  derivointisäännöt,  alkeisfunktioiden derivaatat

Kansisivu  Sisältö  Hakemisto

Yksinkertaisessa populaatiomallissa voidaan ajatella, että populaation lisäys aikavälillä t on suoraan verrannollinen populaation sen hetkiseen kokoon ja aikavälin pituuteen. Jos populaation koko ajanhetkellä t on p(t), on siis

p = p(t + t) - p(t) = kp(t)t,

missä verrannollisuuskerroin k on positiivinen vakio.

Tällöin on

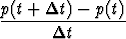= kp(t),

mistä rajaprosessilla t 0 päästään populaation käyttäytymistä mallintavaan differentiaaliyhtälöön

p' = kp.

Tämän ratkaisu on

p(t) = Ce^kt,

missä C on vapaasti valittava vakio. Kyseessä on eksponentiaalisen kasvun malli. Vakio C määrätään jälleen alkuehdon perusteella: Jos populaation koko tunnetaan esimerkiksi ajanhetkellä t = 0, on alkuehtona p(0) = p₀ ja saadaan C = p₀.

Esimerkki osoittaa kaikkien mallien yhteisen piirteen: mallilla on rajoituksensa. Populaatiomallissa on käsitelty hyvin yksinkertaisesti populaation kasvun perusteita. Huomioon ei ole lainkaan otettu kuolleisuutta, rajattomasta kasvusta aiheutuvaa ravinnon niukkuutta, sisäisiä kitkatekijöitä (esimerkiksi keskinäistä kilpailua), ulkoisia vihollisia, jne. Mikään malli tuskin huomioikaan kaikkia vaikuttavia tekijöitä, mutta puuttuvien tekijöiden ollessa merkitykseltään mitättömiä, malli antaa hyviä tuloksia. Jokaisella mallilla on siten pätevyysalueensa.

erotusosamäärä  derivaatta  eksponenttifunktio

Kivelä, niinkuin matematiikka, versio 1.12