![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Alkeisfunktiot
Alkeisfunktiot  Trigonometriset funktiot [ 1
2 3 4 5 6 7 ]
Trigonometriset funktiot [ 1
2 3 4 5 6 7 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot
reaalifunktiot
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) trigonometrian kaavat,
trigonometrian kaavat, ![[#]](kuvat/msam10-c-4.gif) kolmio,
kolmio, ![[#]](kuvat/msam10-c-4.gif) kulma
kulma
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Alkeisfunktiot Alkeisfunktiot  Trigonometriset funktiot [ 1
2 3 4 5 6 7 ] Trigonometriset funktiot [ 1
2 3 4 5 6 7 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot reaalifunktiot
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) trigonometrian kaavat, trigonometrian kaavat, ![[#]](kuvat/msam10-c-4.gif) kolmio, kolmio, ![[#]](kuvat/msam10-c-4.gif) kulma kulma
|
|
Mielivaltaisen kulman  trigonometriset funktiot määritellään yksikköympyrän
avulla.
trigonometriset funktiot määritellään yksikköympyrän
avulla.
Yksikköympyrä on origokeskinen ympyrä, jonka säde on = 1. Kulma  sijaitsee
siten, että sen kärki on origossa ja oikea kylki (alkukylki) positiivisella x-akselilla.
Jos vasen kylki (loppukylki) yhtyy oikeaan kylkeen, kulman suuruus on
= 0. Kulma kasvaa, kun loppukylki kiertyy positiiviseen kiertosuuntaan,
so. vastapäivään. Kylki voi kiertyä useita kierroksia, jolloin saadaan miten suuria
kulmia tahansa. Vastaavasti negatiiviseen suuntaan (myötäpäivään) kiertyminen
merkitsee kulman pienenemistä ja negatiivisia kulmia.
sijaitsee
siten, että sen kärki on origossa ja oikea kylki (alkukylki) positiivisella x-akselilla.
Jos vasen kylki (loppukylki) yhtyy oikeaan kylkeen, kulman suuruus on
= 0. Kulma kasvaa, kun loppukylki kiertyy positiiviseen kiertosuuntaan,
so. vastapäivään. Kylki voi kiertyä useita kierroksia, jolloin saadaan miten suuria
kulmia tahansa. Vastaavasti negatiiviseen suuntaan (myötäpäivään) kiertyminen
merkitsee kulman pienenemistä ja negatiivisia kulmia.
Kulman  suuruus mitataan yleensä radiaaneissa puhuttaessa yleisistä
trigonometrisista funktioista.
suuruus mitataan yleensä radiaaneissa puhuttaessa yleisistä
trigonometrisista funktioista.
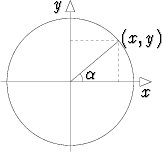
Kulman  kiertyvä loppukylki kohdatkoon yksikköympyrän pisteessä (x, y).
Kuuden trigonometrisen funktion määritelmät ovat tällöin seuraavat:
kiertyvä loppukylki kohdatkoon yksikköympyrän pisteessä (x, y).
Kuuden trigonometrisen funktion määritelmät ovat tällöin seuraavat:
| sini: | sin  = y; = y; | kosini: | cos  = x; = x; |
| tangentti: | tan  = = 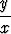 = = 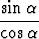 ; ; | kotangentti: | cot  = = 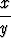 = = 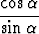 ; ; |
| sekantti: | sec  = =  = = 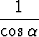 ; ; | kosekantti: | csc  = = 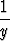 = = 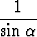 . . |
Jos  on ensimmäisen neljänneksen kulma, so. x > 0, y > 0, yhtyvät sinin, kosinin,
tangentin ja kotangentin määritelmät suorakulmaisen kolmion avulla annettuihin.
Yleiset määritelmät ovat siten aiempien yleistyksiä.
on ensimmäisen neljänneksen kulma, so. x > 0, y > 0, yhtyvät sinin, kosinin,
tangentin ja kotangentin määritelmät suorakulmaisen kolmion avulla annettuihin.
Yleiset määritelmät ovat siten aiempien yleistyksiä.
Funktiot sini, kosini ja tangentti ovat yleisesti käytettyjä. Kotangentti, sekantti ja kosekantti ovat harvinaisempia, mutta varsinkin kahta viimeistä näkee melko paljon amerikkalaisissa oppikirjoissa. Myös monet matemaattiset tietokoneohjelmistot käyttävät niitä.
![[#]](kuvat/msam10-c-4.gif) kulma (taso-) kulma (taso-)![[#]](kuvat/msam10-c-4.gif) ympyrä ympyrä![[#]](kuvat/msam10-c-4.gif) origo origo![[#]](kuvat/msam10-c-4.gif) origo origo![[#]](kuvat/msam10-c-4.gif) kiertosuunta (positiivinen) kiertosuunta (positiivinen)![[#]](kuvat/msam10-c-4.gif) kiertosuunta (positiivinen) kiertosuunta (positiivinen)![[#]](kuvat/msam10-c-4.gif) radiaani radiaani |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12