![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Alkeisfunktiot
Alkeisfunktiot  Trigonometriset funktiot [ 1
2 3 4 5 6 7 ]
Trigonometriset funktiot [ 1
2 3 4 5 6 7 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot
reaalifunktiot
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) trigonometrian kaavat,
trigonometrian kaavat, ![[#]](kuvat/msam10-c-4.gif) kolmio,
kolmio, ![[#]](kuvat/msam10-c-4.gif) kulma
kulma
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Alkeisfunktiot Alkeisfunktiot  Trigonometriset funktiot [ 1
2 3 4 5 6 7 ] Trigonometriset funktiot [ 1
2 3 4 5 6 7 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot reaalifunktiot
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) trigonometrian kaavat, trigonometrian kaavat, ![[#]](kuvat/msam10-c-4.gif) kolmio, kolmio, ![[#]](kuvat/msam10-c-4.gif) kulma kulma
|
|
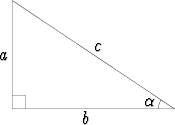
Olkoon  suorakulmaisen kolmion terävä kulma, a tämän vastainen kateetti, b
viereinen kateetti ja c kolmion hypotenuusa. Kulman
suorakulmaisen kolmion terävä kulma, a tämän vastainen kateetti, b
viereinen kateetti ja c kolmion hypotenuusa. Kulman  trigonometriset funktiot
määritellään seuraavina sivujen suhteina:
trigonometriset funktiot
määritellään seuraavina sivujen suhteina:
| sini: | vastaisen kateetin suhde hypotenuusaan eli sin  = a/c; = a/c; |
| kosini: | viereisen kateetin suhde hypotenuusaan eli cos  = b/c; = b/c; |
| tangentti: | vastaisen kateetin suhde viereiseen eli tan  = a/b; = a/b; |
| kotangentti: | viereisen kateetin suhde vastaiseen eli cot  = b/a. = b/a. |
Trigonometrisia funktioita on kaksi muutakin, mutta suorakulmaisen kolmion käsittelyyn riittävät edellä olevat.
Koska suorakulmaisen kolmion terävä kulma  on välillä 0o <
on välillä 0o <  < 90o, antaa
edellä oleva funktioiden määrittelyn vain tällä välillä.
< 90o, antaa
edellä oleva funktioiden määrittelyn vain tällä välillä.
Pythagoraan lauseen mukaan on a2 + b2 = c2, jolloin
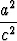 +
+ 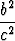 = 1 eli sin2
= 1 eli sin2 + cos2
+ cos2 = 1.
= 1.
(Yleisesti on tapana kirjoittaa sin2 merkityksessä (sin
merkityksessä (sin  )2. Jälkimmäinen tapa
saattaisi kyllä olla johdonmukaisempi.)
)2. Jälkimmäinen tapa
saattaisi kyllä olla johdonmukaisempi.)
Jos suorakulmaisen kolmion toinen terävä kulma on  , niin toinen on 90o -
, niin toinen on 90o -  .
Edellä käytetyin merkinnöin on tällöin
.
Edellä käytetyin merkinnöin on tällöin
sin(90o -  ) = b/c = cos
) = b/c = cos  ja tan(90o -
ja tan(90o -  ) = b/a = cot
) = b/a = cot 
ts. kulman  kosini on sama kuin komplementtikulman 90o -
kosini on sama kuin komplementtikulman 90o -  sini, samoin
kotangentti on komplementtikulman tangentti.
sini, samoin
kotangentti on komplementtikulman tangentti.
![[#]](kuvat/msam10-c-4.gif) kolmio kolmio![[#]](kuvat/msam10-c-4.gif) kulma (terävä) kulma (terävä)![[#]](kuvat/msam10-c-4.gif) kateetti kateetti![[#]](kuvat/msam10-c-4.gif) hypotenuusa hypotenuusa![[#]](kuvat/msam10-c-4.gif) funktio funktio![[#]](kuvat/msam10-c-4.gif) Pythagoraan lause Pythagoraan lause![[#]](kuvat/msam10-c-4.gif) kulma (komplementti-) kulma (komplementti-) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12