Kolmio: perusominaisuudet

Sisällön pääryhmät -->

Kulma, kolmio, monikulmio ja -tahokas -->

Kolmio [ 1 2 3 4 5 6 7 8 9 10 11 ]
ESITIEDOT: [#]

piste,

suora,

kulma
KATSO MYÖS: [#]

geometriset probleemat, [#]

Pythagoraan lause, [#]

monikulmiot

Kansisivu

Sisältö

Hakemisto

Kolmio: perusominaisuudet

Yksinkertaisin monikulmio on kolmio, joka muodostuu kolmesta pisteestä, kolmion kärjistä, ja näitä yhdistävistä janoista, kolmion sivuista. Kussakin kärjessä kohtaavien sivujen välissä on yksi kolmion kulmista.

Toisin kuin muut monikulmiot kolmio on aina tasokuvio: Jos kolme pistettä eivät ole samalla suoralla, mutta sijaitsevat avaruudessa muutoin miten tahansa, ne määräävät aina tason yksikäsitteisesti. Pisteiden määräämä kolmio sijaitsee tässä tasossa.

Paralleeliaksioomasta seuraa, että minkä tahansa (euklidisen) kolmion kulmien summa on 180^o.

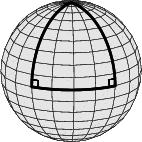
Epäeuklidisessa geometriassa paralleeliaksiooma ei kuitenkaan ole voimassa eikä kolmion kulmien summa myöskään ole 180^o. Esimerkkinä olkoon pallokolmio, joka muodostuu pallon päiväntasaajan kaaresta sekä kahdesta navalta päiväntasaajalle ulottuvasta meridiaanikaaresta, joiden välinen aste-ero on . Kolmion kulmien summa on tällöin 180^o + .

Tavallisen (euklidisen) kolmion sivujen pituuksille pätee seuraava: Kahden sivun summa on suurempi kuin kolmas sivu. Kahden sivun erotus on pienempi kuin kolmas sivu.

Täten muodostuvia epäyhtälöitä kutsutaan kolmioepäyhtälöiksi ja niillä on tavattoman paljon yleistyksiä monille matematiikan aloille. Esimerkiksi reaali- tai kompleksilukujen itseisarvoja koskevissa epäyhtälöissä |z₁ + z₂| < |z₁| + |z₂| ja ||z₁| - |z₂|| < |z₁ + z₂| tai vektoreiden pituuksia koskevissa epäyhtälöissä |a + b| < |a| + |b| ja ||a| - |b|| < |a + b| on kyse samasta asiasta. Lukija piirtäköön kuvan!