Sisällön pääryhmät Käyrät ja pinnat Pallo [ 1 2 3 ] ESITIEDOT:  pinta,  ympyrä KATSO MYÖS:  toisen asteen pinnat,  geometria

Kansisivu  Sisältö  Hakemisto

Geodeettiseksi viivaksi jollakin pinnalla kutsutaan käyrää, joka antaa lyhimmän pintaa pitkin kulkevan tien kahden annetun pisteen välillä. Voidaan osoittaa, että pallon geodeettisia viivoja ovat isoympyröiden kaaret.

Lyhin pallon pintaa pitkin kulkeva tie kahden pisteen välillä on siis näitä yhdistävä isoympyrän kaari. Taso, jossa kaari sijaitsee, määräytyy kolmen pisteen avulla: kaaren päätepisteet ja pallon keskipiste.

Pallon pinnalle voidaan muodostaa elliptinen epäeuklidinen geometria pitämällä isoympyröitä tämän geometrian suorina. Ajatus on sikäli luonnollinen, että tavallisessa tasogeometriassa kahden pisteen välinen lyhin tie on suoran osa, jana. Pallonpintageometriassa lyhin tie on vastaavalla tavalla tämän geometrian suoran osa, isoympyrän kaari.

Pallokolmio on pallonpintageometrian kolmio, jonka sivut ovat isoympyröiden kaaria. Sekä kolmion sivuja — kaaria — että sen kulmia voidaan siten mitata kulmamitoilla, esimerkiksi asteilla. Pallokolmioiden laskemista kutsutaan pallotrigonometriaksi.

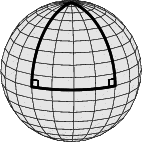
Voidaan osoittaa, että pallokolmioiden kulmien summa on aina > 180^o. Esimerkiksi jos pallokolmion sivuiksi otetaan päiväntasaajan kaari ja kaksi pohjoisnavalta päiväntasaajalle ulottuvaa meridiaanikaarta, saadaan pallokolmio, jonka kulmien summa on 90^o + 90^o + = 180^o + , missä on meridiaanikaarten välinen pituusaste-ero.

pinta  käyrä (avaruus-)  taso  geometria (epäeuklidinen)  geometria (epäeuklidinen)  suora  pallokolmio  pallokolmio  kulma (taso-)  kolmio

Kivelä, niinkuin matematiikka, versio 1.12