Sisällön pääryhmät Geometrian peruskäsitteet Geometria [ 1 2 3 4 ] ESITIEDOT: KATSO MYÖS:  geometriset probleemat,  piste,  suora

Kansisivu  Sisältö  Hakemisto

Geometriaa, so. pisteiden ja suorien muodostamaa järjestelmää sanotaan euklidiseksi geometriaksi, jos siinä on voimassa paralleeliaksiooma, ts. suoran ulkopuolella olevan pisteen kautta voidaan piirtää täsmälleen yksi kyseisen suoran suuntainen suora. Jos näin ei ole, kyseessä on epäeuklidinen geometria.

Yksinkertaisin euklidisen geometrian malli, so. järjestelmä, joka toteuttaa euklidiset aksioomat, on tavallinen xy-taso. Pisteitä ovat tällöin lukuparit (x, y), so. pisteet ilmaistaan koordinaateillaan. Suorat määritellään yhtälöillä: ax + by + c = 0 (missä ainakin toinen luvuista a, b on 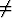0) on suora, jolle kuuluvat ne pisteet, joiden koordinaatit toteuttavat yhtälön. On yksinkertainen algebrallinen lasku osoittaa, että paralleeliaksiooma on voimassa.

Esimerkki epäeuklidisesta geometriasta saadaan tarkastelemalla geometriaa pallon pinnalla. Tämän geometrian pisteet ovat pallon pinnan pisteitä. Suorat ovat pallon pinnalla olevia isoympyröitä, so. ympyröitä, joiden säde on sama kuin pallon säde ja jotka saadaan leikkaamalla pallopintaa pallon keskipisteen kautta kulkevalla tasolla. Kaksi tällaista ympyrää — pallonpintageometrian suoraa — leikkaa toisensa aina, jopa kahdessa vastakkaisilla puolilla palloa olevassa pisteessä. Minkään suoran minkään ulkopuolisen pisteen kautta ei siis voida asettaa suoraa, joka ei leikkaisi kyseistä suoraa! Tällaista epäeuklidista geometriaa kutsutaan elliptiseksi.

Epäeuklidinen geometria voi olla myös hyperbolinen, jolloin suoran ulkopuolisen pisteen kautta voidaan asettaa äärettömän monta suoraa, jotka eivät kohtaa alkuperäistä suoraa missään pisteessä, ts. ovat sen suuntaisia.

koordinaatti  suora (yhtälö)  pallo  isoympyrä  geodeettinen viiva

Kivelä, niinkuin matematiikka, versio 1.12