Pisteen identifiointi

Sisällön pääryhmät -->

Geometrian peruskäsitteet -->

Piste [ 1 2 3 ]
ESITIEDOT: [#]

vektori,

koordinaatistot
KATSO MYÖS: [#]

geometria, [#]

Pythagoraan lause, [#]

vektorialgebra, [#]

geometriset probleemat

Kansisivu

Sisältö

Hakemisto

Pisteen identifiointi

Piste on yksinkertaisin geometrinen peruskäsite. Sitä ei varsinaisesti voida määritellä. Eukleideen Stoikheia-teoksessa esittämä atomistinen määritelmä — piste on se, jolla ei ole osaa — ei oikeastaan ole määritelmä. Sehän ei luonnehdi käsitettä loogisessa mielessä aiemmin määriteltyjen käsitteiden avulla.

Käytännöllisissä tehtävissä voidaan tyytyä ajattelemaan pisteitä havainnollisen mielikuvan mukaisesti ulottuvuuksia vailla olevina kynän kärjen jälkinä.

Puhtaassa synteettisessä taso- tai avaruusgeometriassa, jossa geometrisia kuvioita tarkastellaan ilman algebrallisia apuvälineitä, pisteitä merkitään vain niiden symboleilla. Nämä ovat yleensä isoja latinalaisia kirjaimia: A, B, C, ..., P , Q, jne.

Mikäli jokin piste kiinnitetään origoksi O, voidaan pisteet identifioida paikkavektoreillaan. Paikkavektorin edustajana on suuntajana, joka alkaa origosta ja päättyy ko. pisteeseen. Piste P voidaan siten antaa ilmoittamalla sen paikkavektori r = --->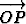
OP .

Paikkavektoreiden käyttö mahdollistaa vektorialgebran käytön geometriassa. Jos tasoon tai avaruuteen kiinnitetään origon lisäksi koordinaattiakselit, voidaan pisteet ilmaista koordinaattien avulla. Yleisimmin käytetään suorakulmaisia koordinaatteja, mutta mikäli tarkasteltava tilanne on tasossa ympyräsymmetrinen, avaruudessa pallo- tai lieriösymmetrinen, on luontevaa käyttää tason napakoordinaatteja, avaruuden pallo- tai lieriökoordinaatteja. Muunkinlaiset koordinaattijärjestelmät voivat tilanteen geometrian mukaan tulla kysymykseen.

Koordinaatteja käytettäessä voidaan geometriaan soveltaa ns. analyyttisen geometrian menetelmiä. Tällöin geometrisia olioita käsitellään niiden yhtälöiden avulla.