Sisällön pääryhmät Kulma, kolmio, monikulmio ja -tahokas Pythagoraan lause [ 1 2 3 ] ESITIEDOT:  kolmio KATSO MYÖS:  vektorigeometriaa

Kansisivu  Sisältö  Hakemisto

Pythagoraan lauseen mukaan suorakulmaisen kolmion kateettien pituuksien a ja b neliöiden summa on hypotenuusan pituuden c neliö:

a² + b² = c².

Lause voidaan alkeellisesti todistaa tarkastelemalla neliötä, jonka sivun pituus on a + b ja piirtämällä sen sisään neljä suorakulmaista kolmiota kahdella eri tavalla:

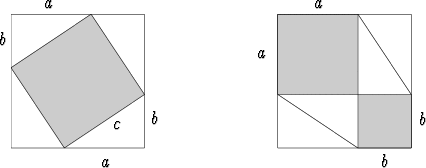
Varjostetut alueet ovat neliöitä, joiden alat ovat a², b² ja c². Näiden ulkopuolelle jäävä alue kummassakin isossa neliössä on sama, neljä samanlaista suorakulmaista kolmiota, jolloin myös varjostettujen alueiden alat ovat samat: c² = a² + b².

Lause voidaan todistaa myös vektorialgebralla: Jos a ja b ovat kateettien vektoriesitykset, niin hypotenuusa on a - b. Hypotenuusan pituuden neliö on tällöin

c² = (a - b) ^. (a - b) = a ^. a + b ^. b - 2a ^. b = a² + b²,

koska a ^. b = 0 kolmion suorakulmaisuuden takia.

Pythagoraan lause on erikoistapaus kosinilauseesta.

kolmio  kateetti  hypotenuusa  geometria (vektori-)  skalaaritulo  kosinilause

Kivelä, niinkuin matematiikka, versio 1.12