![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Kulma, kolmio, monikulmio ja -tahokas
Kulma, kolmio, monikulmio ja -tahokas  Pythagoraan lause [ 1 2 3 ]
Pythagoraan lause [ 1 2 3 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) kolmio
kolmio
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) vektorigeometriaa
vektorigeometriaa
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Kulma, kolmio, monikulmio ja -tahokas Kulma, kolmio, monikulmio ja -tahokas  Pythagoraan lause [ 1 2 3 ]
Pythagoraan lause [ 1 2 3 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) kolmio kolmio
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) vektorigeometriaa vektorigeometriaa
|
|
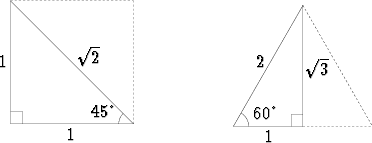
Soveltamalla Pythagoraan lausetta tasakylkiseen suorakulmaiseen kolmioon, jossa kummankin kateetin pituus on a ja hypotenuusan pituus on x, saadaan
a2 + a2 = x2,
jolloin x = a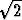 .
.
Jos tasasivuinen kolmio, jonka sivun pituus on 2a, jaetaan korkeusjanalla kahtia, saadaan kaksi suorakulmaista kolmiota, joissa hypotenuusan pituus on 2a ja lyhyempi kateetti symmetrian takia a/2. Jos pitempi kateetti eli kolmion korkeusjana on x, Pythagoraan lause antaa
a2 + x2 = 4a2,
mistä seuraa x = a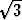 .
.
Saadaan siis seuraavat tulokset:
Jos suorakulmaisen kolmion molemmat terävät kulmat ovat 45 astetta, niin
kateettien ja hypotenuusan suhde on 1 : 1 : 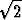 .
.
Jos suorakulmaisen kolmion terävät kulmat ovat 30 ja 60 astetta, niin kateettien
ja hypotenuusan suhde on 1 : 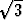 : 2.
: 2.
![[#]](kuvat/msam10-c-4.gif) tasakylkinen tasakylkinen![[#]](kuvat/msam10-c-4.gif) kateetti kateetti![[#]](kuvat/msam10-c-4.gif) hypotenuusa hypotenuusa![[#]](kuvat/msam10-c-4.gif) tasasivuinen tasasivuinen![[#]](kuvat/msam10-c-4.gif) korkeusjana korkeusjana![[#]](kuvat/msam10-c-4.gif) kulma
(terävä) kulma
(terävä) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12