![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Geometrian peruskäsitteet
Geometrian peruskäsitteet  Geometria [ 1
2 3 4 ]
Geometria [ 1
2 3 4 ]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) geometriset probleemat,
geometriset probleemat, ![[#]](kuvat/msam10-c-4.gif) piste,
piste, ![[#]](kuvat/msam10-c-4.gif) suora
suora
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Geometrian peruskäsitteet Geometrian peruskäsitteet  Geometria [ 1
2 3 4 ] Geometria [ 1
2 3 4 ]
ESITIEDOT: KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) geometriset probleemat, geometriset probleemat, ![[#]](kuvat/msam10-c-4.gif) piste, piste, ![[#]](kuvat/msam10-c-4.gif) suora suora
|
|
Projektiivisessa geometriassa tutkitaan suorien ja tasojen keskinäistä leikkaamista kiinnittämättä huomiota mitallisiin ominaisuuksiin. Tämänkin geometrian alan historia on pitkä. Merkittäviä nimiä ovat Pappos Aleksandrialainen 300-luvulta, ranskalaiset Girard Desargues ja Blaise Pascal 1600-luvulta, samoin ranskalaiset Charles-Julien Brianchon ja Jean-Victor Poncelet 1800-luvun alusta.
Esimerkkinä projektiivisen geometrian lauseista olkoon seuraava Pappoksen lause: Olkoon annettuna kaksi suoraa tasossa; toiselta valitaan pisteet A1, B1, C1 ja toiselta pisteet A2, B2, C2. Olkoon piste R suorien A1B2 ja A2B1 leikkauspiste, piste S vastaavasti suorien B1C2 ja B2C1 leikkauspiste ja piste T suorien C1A2 ja C2A1. Tällöin pisteet R, S ja T ovat samalla suoralla.
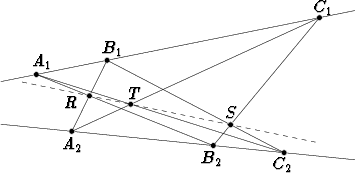
Jotta Pappoksen lause olisi poikkeuksetta voimassa, on suorien leikkauspisteen käsitettä täydennettävä sitä tapausta varten, että suorat sattuvat olemaan yhdensuuntaisia, jolloin leikkauspistettä ei tavanomaisessa mielessä ole. Projektiivisessa geometriassa otetaan tätä varten käyttöön ns. ’äärettömän kaukaiset pisteet’: kahden yhdensuuntaisen suoran sanotaan leikkaavan äärettömän kaukaisessa pisteessä, joka sijaitsee suorien suunnassa.
Projektiivista geometriaa voidaan myös käsitellä algebran keinoin (eräänlaisena analyyttisena geometriana).
![[#]](kuvat/msam10-c-4.gif) Pappos Pappos![[#]](kuvat/msam10-c-4.gif) Desargues Desargues![[#]](kuvat/msam10-c-4.gif) Pascal Pascal![[#]](kuvat/msam10-c-4.gif) Poncelet
(geometria) Poncelet
(geometria)![[#]](kuvat/msam10-c-4.gif) Poncelet Poncelet![[#]](kuvat/msam10-c-4.gif) geometria (analyyttinen) geometria (analyyttinen) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12