![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Käyrät ja pinnat
Käyrät ja pinnat  Pallo [ 1 2 3
]
Pallo [ 1 2 3
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) pinta,
pinta, ![[#]](kuvat/msam10-c-4.gif) ympyrä
ympyrä
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) toisen asteen pinnat,
toisen asteen pinnat, ![[#]](kuvat/msam10-c-4.gif) geometria
geometria
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Käyrät ja pinnat Käyrät ja pinnat  Pallo [ 1 2 3
] Pallo [ 1 2 3
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) pinta, pinta, ![[#]](kuvat/msam10-c-4.gif) ympyrä ympyrä
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) toisen asteen pinnat, toisen asteen pinnat, ![[#]](kuvat/msam10-c-4.gif) geometria geometria
|
|
Pallo on pinta, jonka kaikki pisteet ovat vakioetäisyydellä kiinteästä pisteestä, pallon keskipisteestä. Vakioetäisyys on pallon säde.
Nimitys pallo voi tarkoittaa joko pallopintaa tai pallopinnan rajoittamaa avaruuden osaa.
Pythagoraan lauseesta seuraa, että kahden avaruuspisteen (a, b, c) ja (x, y, z)
välinen etäisyys on 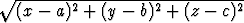 , jolloin pallopinnan yhtälöksi
saadaan
, jolloin pallopinnan yhtälöksi
saadaan
(x - a)2 + (y - b)2 + (z - c)2 = R2,
missä (a, b, c) on pallon keskipiste ja R sen säde.
Pallon yhtälöä voidaan tutkia samaan tapaan kuin ympyrän yhtälöä. Erityisesti jos toisen asteen pinnan yhtälössä termeillä x2, y2 ja z2 on sama kerroin ja yz-, zx- ja xy-termit puuttuvat, yhtälö esittää joko palloa, pistettä tai ei mitään.
Esimerkiksi: Yhtälö
x2 + y2 + z2 + 4x - 2y + 6z - 2 = 0
voidaan binomin neliöiksi täydentämällä saattaa muotoon
| (x2 + 4x + 4) + (y2 - 2y + 1) + (z2 + 6z + 9) - 4 - 1 - 9 - 2 = 0 eli | |||
| (x + 2)2 + (y - 1)2 + (z + 3)2 = 16. |
![[#]](kuvat/msam10-c-4.gif) pallo pallo![[#]](kuvat/msam10-c-4.gif) pallo (tilavuus) pallo (tilavuus)![[#]](kuvat/msam10-c-4.gif) pallo (ala) pallo (ala)![[#]](kuvat/msam10-c-4.gif) pinta pinta![[#]](kuvat/msam10-c-4.gif) Pythagoraan lause Pythagoraan lause![[#]](kuvat/msam10-c-4.gif) koordinaatisto
(xyz-) koordinaatisto
(xyz-)![[#]](kuvat/msam10-c-4.gif) etäisyys (pisteiden) etäisyys (pisteiden)![[#]](kuvat/msam10-c-4.gif) ympyrä ympyrä![[#]](kuvat/msam10-c-4.gif) pinta (toisen asteen) pinta (toisen asteen)![[#]](kuvat/msam10-c-4.gif) binomi binomi |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12