Ulkoa muistettavat peruskaavat

Sisällön pääryhmät -->

Alkeisfunktiot -->

Trigonometrian kaavat [ 1 2 3 4 5 6 ]
ESITIEDOT: [#]

trigonometriset funktiot
KATSO MYÖS:

Kansisivu

Sisältö

Hakemisto

Ulkoa muistettavat peruskaavat

Trigonometrisia funktioita koskevia kaavoja on paljon. Seuraavassa esitetään tärkeimmät ja lyhyet ohjeet niiden muistamiseen. Varsinaisesti ulkoa opeteltavia kaavoja lienee vain kolme: sinin ja kosinin neliösumma on = 1, sinin ja kosinin yhteenlaskukaavat.

On huomattava, että kaavoja usein tarvitaan myös oikealta vasemmalle luettuina. Jonkin lausekkeen sieventäminen nimittäin saattaa edellyttää sen tunnistamista jonkin kaavan vasemman tai oikean puolen tyyppiä olevaksi.

Sinin ja kosinin määrittely yksikköympyrän avulla antaa kaikilla kulmilla x voimassa olevan sinin ja kosinin peruskaavan

sin²x + cos²x = 1

Vektorialgebraa, lähinnä skalaari- ja vektorituloa käyttäen saadaan sinin ja kosinin yhteenlaskukaavat:

sin(x + y)	=	sin x cos y + cos x sin y
cos(x + y)	=	cos x cos y - sin x sin y

Vastaavat vähennyslaskukaavat sin(x - y) = ... ja cos(x - y) = ... saadaan edellä olevista kirjoittamalla y:n paikalle -y ja käyttämällä kaavan oikealla puolella hyväksi sinifunktion parittomuutta ja kosinifunktion parillisuutta. Jakamalla nämä kaavat puolittain ja supistamalla oikea puoli lausekkeella cos x cos y saadaan yhteenlaskukaava tangentille

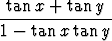
tan(x + y) = -tanx-+-tan-y-
1 - tan xtan y

(Tämän kaavan ulkoa opetteluun tuskin on tarvetta. Kaavan johto, so. sinin ja kosinin kaavojen puolittainen jakaminen ja senjälkeinen supistaminen on tehtävissä varsin nopeasti.)