Sisällön pääryhmät Alkeisfunktiot Trigonometrian kaavat [ 1 2 3 4 5 6 ] ESITIEDOT:  trigonometriset funktiot KATSO MYÖS:

Kansisivu  Sisältö  Hakemisto

Yhtälö sin 2x = cos x voidaan ratkaista kahdellakin tavalla.

1) Sinin kaksinkertaisen kulman kaavan avulla yhtälö saadaan muotoon
2 sin x cos x = cos x, mikä ilmeisesti toteutuu, jos cos x = 0 tai sin x = .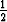

Koska cos(/2) = 0, vastaa edellinen tapaus yhtälöä cos x = cos(/2), mistä seuraa x = ±/2 + 2k. Tämä voidaan myös kirjoittaa muotoon

x = /2 + n.

Luvut k ja n ovat kokonaislukuja.

Koska sin(/6) = , saadaan jälkimmäisestä vaihtoehdosta sin x = sin(/6), jolloin

x = /6 + 2k tai x = - /6 + 2k = 5/6 + 2k.

Yhden kierroksen alueella on siis seuraavan kuvion mukaiset juuret:

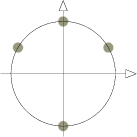
2) Yhtälö voidaan vaihtoehtoisesti kirjoittaa muotoon sin 2x = sin(/2 - x), jolloin saadaan

2x = /2 - x + 2k tai 2x = - (/2 - x) + 2k.

Näistä voidaan ratkaista x:

x = /6 + 2k/3 tai x = /2 + 2k.

Tulos on sama kuin edellä, vaikka juuret onkin ryhmitelty hieman eri tavoin.

sini  kosini

Kivelä, niinkuin matematiikka, versio 1.12