![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Alkeisfunktiot
Alkeisfunktiot  Trigonometrian kaavat [ 1
2 3 4 5 6 ]
Trigonometrian kaavat [ 1
2 3 4 5 6 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) trigonometriset funktiot
trigonometriset funktiot
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Alkeisfunktiot Alkeisfunktiot  Trigonometrian kaavat [ 1
2 3 4 5 6 ] Trigonometrian kaavat [ 1
2 3 4 5 6 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) trigonometriset funktiot trigonometriset funktiot
KATSO MYÖS: |
|
Yhtälö sin x + cos x = 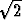 voidaan ratkaista sijoittamalla
voidaan ratkaista sijoittamalla
cos x = 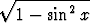 ,
,
jolloin saadaan juuriyhtälö tuntemattomana sin x. Tämän ratkaisu tapahtuu siirtämällä termejä yhtälössä sopivasti ja korottamalla saatu yhtälö puolittain neliöön. Seurauksena voi olla (ja onkin) että saadaan ylimääräisiä juuria, jotka eivät toteutakaan alkuperäistä yhtälöä.
Neliöön korotus voidaan kuitenkin tehdä yksinkertaisemminkin. Korottamalla alkuperäinen yhtälö suoraan neliöön saadaan
sin2x + cos2x + 2 sin x cos x = 2, mistä seuraa sin 2x = 1.
Tällöin 2x =  /2 + 2k
/2 + 2k eli x =
eli x =  /4 + k
/4 + k . Neliöön korotus on tällöinkin tuonut
mukanaan ylimääräisiä juuria. Tarkistus osoittaa, että kelvollisia ovat ainoastaan
arvot
. Neliöön korotus on tällöinkin tuonut
mukanaan ylimääräisiä juuria. Tarkistus osoittaa, että kelvollisia ovat ainoastaan
arvot
x =  /4 + 2k
/4 + 2k .
.
Ratkaisu voidaan myös perustaa toisenlaiseen ideaan:
Jakamalla alkuperäinen yhtälö luvulla 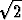 saadaan
saadaan
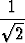 sin x + sin x + 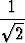 cos x = 1 eli cos x = 1 eli | ||||
cos 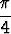 sin x + sin sin x + sin 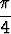 cos x = 1, cos x = 1, |
 /4) = 1. Tällöin
x +
/4) = 1. Tällöin
x +  /4 =
/4 =  /2 + 2k
/2 + 2k , mikä antaa saman ratkaisun kuin edellä.
, mikä antaa saman ratkaisun kuin edellä. ![[#]](kuvat/msam10-c-4.gif) yhtälö (juuri-) yhtälö (juuri-) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12