Sisällön pääryhmät Alkeisfunktiot Trigonometrian kaavat [ 1 2 3 4 5 6 ] ESITIEDOT:  trigonometriset funktiot KATSO MYÖS:

Kansisivu  Sisältö  Hakemisto

Mikä tahansa trigonometrinen funktio voidaan lausua minkä tahansa muun trigonometrisen funktion avulla. Nämä kaavat voidaan johtaa käyttämällä edellä johdettuja kaavoja hyväksi, mutta helpoimmin ne voidaan löytää tarkastelemalla sopivaa suorakulmaista kolmiota. Olkoon esimerkkinä muiden funktioiden lausuminen tangentin avulla.

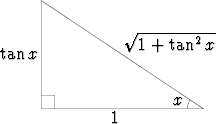
Tarkastellaan suorakulmaista kolmiota, jonka toinen terävä kulma on x ja tämän viereisen kateetin pituus 1. Vastainen kateetti on tällöin tan x tangentin määritelmän mukaan ja hypotenuusa 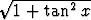Pythagoraan lauseen mukaan. Kolmiosta voidaan lukea suoraan muut trigonometriset funktiot:

sin x = 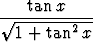, cos x = .

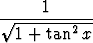Päättelyssä on luonnollisestikin 0 < x < /2. Tulos on kuitenkin pätevä muillekin kulmille x, kun neliöjuurten eteen lisätään ±-merkit. Siis

sin x = ±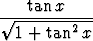, cos x = ±.

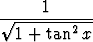Kumpi merkki on oikea, riippuu siitä yksikköympyrän neljänneksestä, missä kulma x on. Se on siis pääteltävä erikseen jokaisessa yksityistapauksessa esimerkiksi trigonometristen funktioiden merkkikaavioiden avulla.

Samantyyppisellä menettelyllä voidaan trigonometriset funktiot lausua muunkin funktion kuin tangentin avulla. Tällöin on vain valittava sopivasti sivu, jonka pituudeksi otetaan 1.

trigonometrinen funktio (yleinen määritelmä)  kolmio  kulma (terävä)  kateetti  hypotenuusa  Pythagoraan lause  neliöjuuri  trigonometrinen funktio (merkkikaavio)

Kivelä, niinkuin matematiikka, versio 1.12