Sisällön pääryhmät Kulma, kolmio, monikulmio ja -tahokas Kulma [ 1 2 3 4 ] ESITIEDOT:  piste,  suora,  taso,  ympyrä,  pallo KATSO MYÖS:  vektorialgebra

Kansisivu  Sisältö  Hakemisto

Täsmällinen kulman suuruuden määrittely edellyttää, että toinen kulman kyljistä sovitaan alkukyljeksi ja toinen loppukyljeksi. Kulman suuruus on positiivinen, jos alkukyljeltä loppukyljelle kierretään vastapäivään, ns. positiiviseen kiertosuuntaan. Myötäpäivään eli negatiiviseen kiertosuuntaan kierrettäessä kulman suuruus on negatiivinen. Sallittua on myös kiertää ylimääräisiä täysiä kierroksia, jolloin kulman asteluku voi olla yli 360^o tai alle -360^o.

Paitsi asteita kulman suuruuden mittaamiseen käytetään muitakin yksikköjä. Eräs mahdollisuus on käyttää ns. graadeja, jolloin täyden kulman suuruus on 400 graadia. Toinen eräissä yhteyksissä yleisesti käytetty yksikkö on piiru, jolloin täyden kulman suuruus on 6000 piirua.

Teoreettisissa yhteyksissä, mm. matematiikassa yleisimmin käytetty yksikkö on radiaani. Kulman suuruus radiaaneissa saadaan piirtämällä kulman aukeaman alueelle ympyränkaari keskipisteenä kulman kärki. Kulman suuruus radiaaneina on kulman aukeamaan jäävän ympyränkaaren pituuden ja ympyrän säteen suhde. Täyden kulman suuruus on ympyrän kehän pituus jaettuna säteellä, siis 2.

Asteiden ja radiaanien välinen vastaavuus saadaan yksinkertaisesta verrannosta

= .

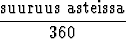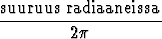Erityisesti on 1 rad 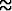57.296^o.

Matemaattiset tietokoneohjelmat edellyttävät yleensä, että trigonometristen funktioiden argumentit annetaan radiaaneissa. Jos halutaan käyttää asteita, on käyttäjän itsensä huolehdittava tarvittavasta muunnoksesta. Laskimissa sen sijaan on yleensä erikseen toimintamoodit radiaaneille ja asteille, mahdollisesti muillekin kulmayksiköille.

Trigonometrisille funktioille voidaan muodostaa sarjakehitelmät, joista näiden arvoja voidaan laskea. Nämä on aina tapana esittää sellaisessa muodossa, että argumentin oletetaan olevan radiaaneissa.

kiertosuunta (positiivinen)  kiertosuunta (positiivinen)  ympyrä  verranto  trigonometrinen funktio (yleinen määritelmä)  sarja

Kivelä, niinkuin matematiikka, versio 1.12