Sisällön pääryhmät Lukujonon ja funktion raja-arvo Sarjat [ 1 2 3 4 ] ESITIEDOT:  summa ja tulo,  lukujonot,  lukujonon raja-arvo KATSO MYÖS:  Neperin luku e,  luku

Kansisivu  Sisältö  Hakemisto

Olkoon annettuna äärettömän monen termin lukujono a₁,  a₂,  a₃,  .... Kun jonon kaikki termit lasketaan yhteen, saadaan sarja

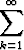a_k.

Termien indeksoinnin alkukohta voi olla muukin kuin 1.

Äärettömän monen termin yhteenlaskeminen on kuitenkin ongelmallista. Jotta operaatio saadaan täsmällisesti määritellyksi, on meneteltävä seuraavasti.

Muodostetaan sarjan osasummat, so. äärellisen monen termin summat, joihin otetaan termejä alusta lähtien jokin äärellinen määrä:

s₁ = a₁, s₂ = a₁ + a₂, s₃ = a₁ + a₂ + a₃, s₄ = a₁ + a₂ + a₃ + a₄,

jne. Yleisesti on n:s osasumma

s_n = 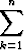a_k, n = 1, 2, 3, ... .

Osasummat s₁,  s₂,  s₃,  ... muodostavat lukujonon. Jos tämä suppenee ja sen raja-arvo on s = lim_ns_n, sanotaan, että sarja 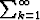a_k suppenee ja sen summa on s.

Jos sarja ei suppene, sen sanotaan hajaantuvan. Hajaantuvalla sarjalla siis jonon s₁, s₂, s₃,  ... luvut joko heilahtelevat mitään arvoa lähestymättä tai karkaavat äärettömyyteen.

Jos sarja 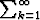a_k suppenee, niin lim_ka_k = 0, ts. suppenevalla sarjalla termit lähestyvät nollaa indeksin kasvaessa. Tämä nähdään helposti: Koska

a_n = 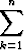a_k - a_k = s_n - s_n-1,

on lim_na_n = lim_ns_n - lim_ns_n-1 = s - s = 0.

Voisi luulla, että myös käänteinen olisi voimassa. Näin ei kuitenkaan ole. Vaikka olisikin lim_ka_k = 0, sarja voi silti hajaantua. Esimerkki (harmoninen sarja) edempänä.

lukujono  summa  summamerkintä  raja-arvo (lukujonon)  harmoninen sarja

Kivelä, niinkuin matematiikka, versio 1.12