Sisällön pääryhmät Lukujonon ja funktion raja-arvo Lukujonon raja-arvo [ 1 2 3 4 5 6 7 ] ESITIEDOT:  lukujonot KATSO MYÖS:  funktion raja-arvo,  Neperin luku e

Kansisivu  Sisältö  Hakemisto

Raja-arvon täsmällinen määrittely merkitsee edellä mainitun lähestymisen käsitteen täsmentämistä ja tekemistä riippumattomaksi siitä, miten nopeasti luvut raja-arvoa lähestyvät.

Vaatimuksena on, että asetetaanpa miten pieni etäisyyskynnys tahansa, luvut a_n tulevat tätä etäisyyttä lähemmäksi raja-arvoa a, kunhan vain jonossa edetään kyllin pitkälle.

Mitä pienempi etäisyyskynnys asetetaan, sitä pidemmälle jonossa yleensä on edettävä, mutta jokaista etäisyyskynnystä kohden löydetään jonosta kohta, josta eteenpäin luvut ovat kynnysarvoa lähempänä raja-arvoa.

Toisin sanoen: Jokaista etäisyyskynnystä (> 0) vastaa indeksiraja n₀ siten, että |a_n - a| < , kun n > n₀.

Itseisarvolauseke |a_n - a| on tässä syytä mieltää lukujen a_n ja a väliseksi etäisyydeksi lukusuoralla.

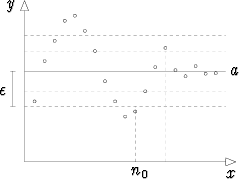
Määritelmä on pätevä myös kompleksilukujen tapauksessa. Erotuksen itseisarvo voidaan nimittäin mieltää pisteiden a_n ja a väliseksi etäisyydeksi kompleksitasossa.

itseisarvo (reaaliluvun)  lukusuora  kompleksiluku  itseisarvo (kompleksiluvun)

Kivelä, niinkuin matematiikka, versio 1.12