Sisällön pääryhmät Lukujonon ja funktion raja-arvo Lukujonon raja-arvo [ 1 2 3 4 5 6 7 ] ESITIEDOT:  lukujonot KATSO MYÖS:  funktion raja-arvo,  Neperin luku e

Kansisivu  Sisältö  Hakemisto

Rekursiivisesti määritelty lukujono

a₁ = 0.5, a_n+1 = ra_n(1 - a_n),  n = 1, 2, 3, ... ,

missä r = 3.75, on esitetty oheisessa kuvassa. Vaaka-akselilla on indeksiarvot, pystyakselilla jonon lukujen arvot.

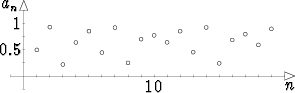
Ilmeisestikään jono ei suppene, mutta pysyy rajoitettuna välille [0, 1]. Yksittäiset luvut riippuvat voimakkaasti ensimmäisen luvun valinnasta eikä jonossa ole havaittavissa jaksollisuutta. Tämän johdosta sen sanotaan käyttäytyvän kaoottisesti.

Koska jono kuitenkin pysyy rajoitettuna, voidaan kysyä, millä välillä sen luvut raja-arvomielessä ovat. Tällöin johdutaan alaraja-arvon ja yläraja-arvon käsitteisiin. Olkoon m_p suurin mahdollinen alaraja niille luvuille, joiden indeksi on > p, ja M_p pienin mahdollinen yläraja samoille luvuille. Näitä merkitään

m_p = inf_n>pa_n, M_p = sup_n>pa_n.

Symbolit inf ja sup ovat lyhenteitä sanoista infimum ja supremum.

Voidaan todistaa, että lukujonoilla m₁,  m₂,  m₃,  ... ja M₁,  M₂,  M₃,  ... on aina (jonon a₁,  a₂,  a₃,  . . . ollessa rajoitettu) olemassa raja-arvot. Näitä kutsutaan alaraja-arvoksi ja yläraja-arvoksi (limes inferior ja limes superior); merkinnät

lim_pm_p = lim inf_na_n, lim_pM_p = lim sup_na_n.

Havainnollisesti sanoen jonon luvut kasautuvat ala- ja yläraja-arvon väliselle alueelle. Jos jono suppenee, ala- ja yläraja-arvo yhtyvät jonon raja-arvoksi.

rekursiivisesti määritelty lukujono

Kivelä, niinkuin matematiikka, versio 1.12