Sisällön pääryhmät Lukujonon ja funktion raja-arvo Lukujonot [ 1 2 3 ] ESITIEDOT:  funktiokäsite KATSO MYÖS:  summa ja tulo,  lukujonon raja-arvo,  sarjat

Kansisivu  Sisältö  Hakemisto

Jos lukujono määritellään antamalla jonon luvulle lauseke indeksin funktiona, esimerkiksi

a_k = 2^k tai a_k = (1 + 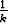)^k,

sanotaan, että jono on määritelty eksplisiittisesti.

Toisena vaihtoehtona on määritellä jono rekursiivisesti, jolloin ilmoitetaan sopiva määrä jonon alkupään lukuja ja yhtälö, joka kertoo, miten seuraava luku lasketaan edellisten avulla. Esimerkiksi määrittely

a₁ = 1,  a₂ = 1, a_k+2 = a_k+1 + a_k,  k = 1, 2, 3, ... ,

antaa ns. Fibonacci’n luvut 1,  1,  2,  3,  5,  8,  13,  21,  34,  55,  89,  ... . Määrittelyn perusteella on selvää, että nämä ovat kaikki kokonaislukuja.

Tämäkin lukujono on mahdollista määritellä myös eksplisiittisesti, vaikka lausekkeen löytäminen ei aivan yksinkertaista olekaan:

a_k = .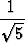

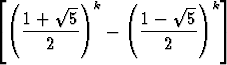Lasketaanpa lauseke millä tahansa indeksin k arvolla, tuloksena on neliöjuurista huolimatta aina Fibonacci’n luku.

Kivelä, niinkuin matematiikka, versio 1.12