![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Lukujonon ja funktion raja-arvo
Lukujonon ja funktion raja-arvo  Lukujonot
[ 1 2 3 ]
Lukujonot
[ 1 2 3 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) funktiokäsite
funktiokäsite
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) summa ja tulo,
summa ja tulo, ![[#]](kuvat/msam10-c-4.gif) lukujonon raja-arvo,
lukujonon raja-arvo, ![[#]](kuvat/msam10-c-4.gif) sarjat
sarjat
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Lukujonon ja funktion raja-arvo Lukujonon ja funktion raja-arvo  Lukujonot
[ 1 2 3 ] Lukujonot
[ 1 2 3 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) funktiokäsite funktiokäsite
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) summa ja tulo, summa ja tulo, ![[#]](kuvat/msam10-c-4.gif) lukujonon raja-arvo, lukujonon raja-arvo, ![[#]](kuvat/msam10-c-4.gif) sarjat sarjat
|
|
Lukujonoa sanotaan aritmeettiseksi, jos jonon kahden peräkkäisen luvun erotus on vakio:
a1 annettu, ak+1 = ak + d, k = 1, 2, 3, ... .
Eksplisiittisessä muodossa tämä on ak = a1 + (k - 1)d, k = 1, 2, 3, ... .
Jono on geometrinen, jos kahden peräkkäisen luvun suhde on vakio:
b1 annettu, bk+1 = qbk, k = 1, 2, 3, ... ,
tai eksplisiittisesti bk = qk-1b1, k = 1, 2, 3, ... .
Sekä aritmeettisen että geometrisen jonon tapauksessa voidaan johtaa lauseke jonon n ensimmäisen luvun summalle. Aritmeettinen summa, so. aritmeettisen jonon n ensimmäisen termin summa, on ensimmäisen ja viimeisen termin keskiarvo kerrottuna termien lukumäärällä:
sn =  ak = n
ak = n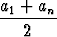 .
.
Geometrinen summa eli geometrisen jonon n ensimmäisen termin summa on hieman vaikeammin miellettävissä:
tn = 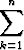 bk = b1
bk = b1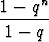 , q
, q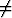 1.
1.
Osoittajassa esintyy siis suhdeluku q korotettuna termien lukumäärän mukaiseen potenssiin. Poikkeuksena on tapaus q = 1, jolloin geometrisen jonon termit ovat kaikki yhtä suuria ja siis tn = nb1.
Aritmeettinen ja geometrinen summa antavat itse asiassa uudet lukujonot:
s1, s2, s3, ... ja t1, t2, t3, ... . Myös s1 ja t1 ovat määriteltyjä edellä olevien
lausekkeiden avulla: Tällöin on ajateltava, että merkintä s1 = 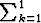 ak
tarkoittaa summaa, joka ei oikeastaan summa olekaan, koska siinä on vain
yksi termi, a1; vastaavasti t1 =
ak
tarkoittaa summaa, joka ei oikeastaan summa olekaan, koska siinä on vain
yksi termi, a1; vastaavasti t1 = 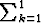 bk.
bk.
![[#]](kuvat/msam10-c-4.gif) summa summa![[#]](kuvat/msam10-c-4.gif) summamerkintä summamerkintä |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12