Sisällön pääryhmät Derivaatta Maksimit ja minimit [ 1 2 3 4 5 ] ESITIEDOT:  reaalifunktiot,  derivaatta KATSO MYÖS:  funktion jatkuvuus,  derivointisäännöt,  alkeisfunktioiden derivaatat

Kansisivu  Sisältö  Hakemisto

Jos derivoituvan reaalifunktion f derivaatta tietyssä pisteessä on positiivinen, f'(x₀) > 0, niin funktion tangentti tässä pisteessä on nouseva ja funktio siis on aidosti kasvava pisteen kohdalla: jos riittävän pienessä pisteen x₀ ympäristössä on x₁ < x₀ < x₂, niin f(x₁) < f(x₀) < f(x₂). (Varovaisuus on tarpeen: Tämä ei ole sama kuin funktion kasvavuus kyseisessä ympäristössä. Hyvä — mutta hieman vaikea — esimerkki on kaikkialla derivoituva funktio f(x) = x + 2x² sin(1/x), f(0) = 0 pisteessä x₀ = 0.)

Vastaavasti jos derivaatta on negatiivinen, f'(x₀) < 0, niin funktio on kohdassa x₀ aidosti vähenevä. Funktiolla f sanotaan olevan paikallinen maksimi pisteessä x₀, jos funktion arvo f(x₀) on suurempi kuin sen arvot pisteen x₀ välittömässä ympäristössä. Vastaavasti määritellään paikallinen minimi.

Paikallista maksimia ja minimiä kutsutaan funktion paikallisiksi ääriarvoiksi; vastaava muuttujan arvo x₀ on ääriarvokohta.

Jos funktio f on ääriarvokohdassa x₀ derivoituva (mitä sen ei tarvitse olla, esim. f(x) = |x| origossa), on sen derivaatta välttämättä = 0. Jos derivaatta nimittäin olisi > 0 tai < 0, olisi funktio edellä sanotun mukaan aidosti kasvava tai vähenevä pisteen ympäristössä eikä kyseessä olisikaan ääriarvo.

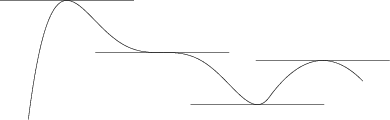
Ääriarvokohdassa derivoituvan funktion kuvaajalla on siis vaakasuora tangentti. Tangentti voi olla vaakasuora muuallakin kuin ääriarvokohdassa, kuten alla oleva kuva osoittaa. Yhtälö f'(x) = 0 antaa siis derivoituvalle funktiolle mahdolliset ääriarvokohdat, mutta yhtälön ratkaisujen joukossa voi olla arvoja, jotka eivät ole ääriarvokohtia.

derivoituvuus  funktio (reaali-)  derivaatta  tangentti (suora)  kasvava (funktio)  kasvava (funktio)  vähenevä (funktio)  vähenevä (funktio)

Kivelä, niinkuin matematiikka, versio 1.12